UNSURE: Unknown Noise level Stein's Unbiased Risk Estimator
Paper and Code
Sep 03, 2024

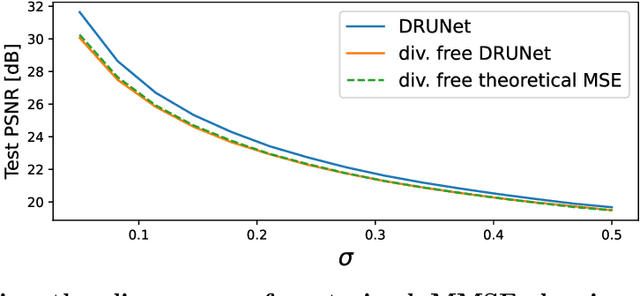

Recently, many self-supervised learning methods for image reconstruction have been proposed that can learn from noisy data alone, bypassing the need for ground-truth references. Most existing methods cluster around two classes: i) Noise2Self and similar cross-validation methods that require very mild knowledge about the noise distribution, and ii) Stein's Unbiased Risk Estimator (SURE) and similar approaches that assume full knowledge of the distribution. The first class of methods is often suboptimal compared to supervised learning, and the second class is often impractical, as the noise level is generally unknown in real-world applications. In this paper, we provide a theoretical framework that characterizes this expressivity-robustness trade-off and propose a new approach based on SURE, but unlike the standard SURE, does not require knowledge about the noise level. Throughout a series of experiments, we show that the proposed estimator outperforms other existing self-supervised methods on various imaging inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge