Unsupervised learning of transcriptional regulatory networks via latent tree graphical models
Paper and Code
Sep 20, 2016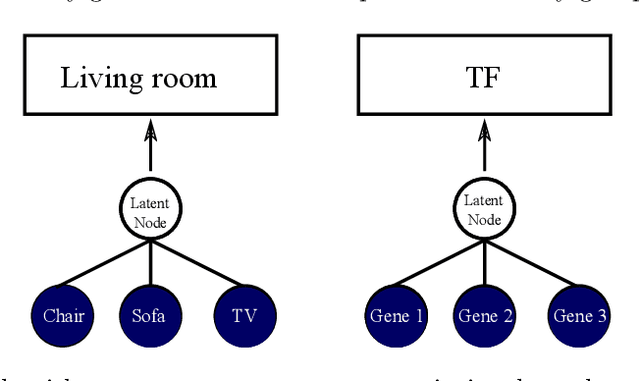

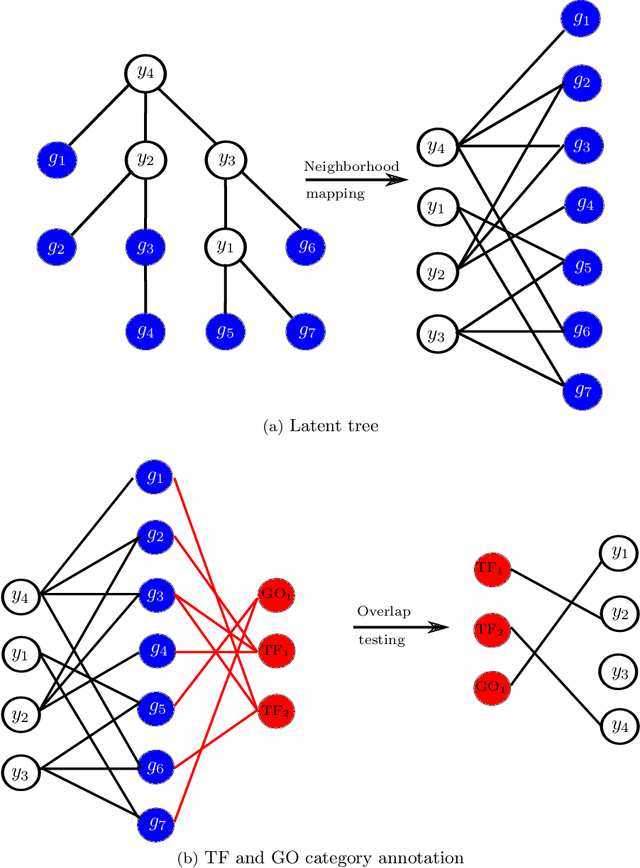
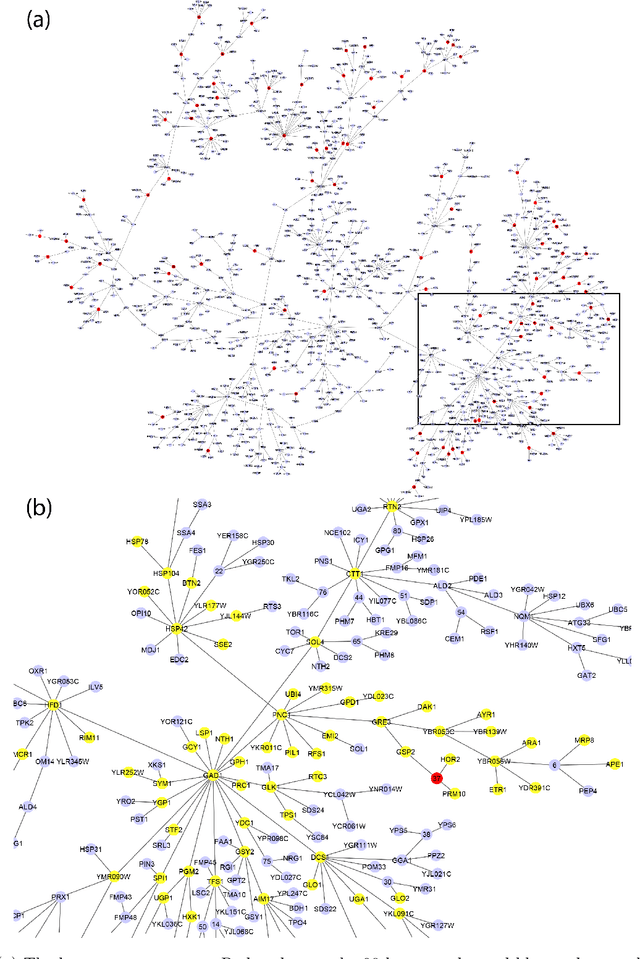
Gene expression is a readily-observed quantification of transcriptional activity and cellular state that enables the recovery of the relationships between regulators and their target genes. Reconstructing transcriptional regulatory networks from gene expression data is a problem that has attracted much attention, but previous work often makes the simplifying (but unrealistic) assumption that regulator activity is represented by mRNA levels. We use a latent tree graphical model to analyze gene expression without relying on transcription factor expression as a proxy for regulator activity. The latent tree model is a type of Markov random field that includes both observed gene variables and latent (hidden) variables, which factorize on a Markov tree. Through efficient unsupervised learning approaches, we determine which groups of genes are co-regulated by hidden regulators and the activity levels of those regulators. Post-processing annotates many of these discovered latent variables as specific transcription factors or groups of transcription factors. Other latent variables do not necessarily represent physical regulators but instead reveal hidden structure in the gene expression such as shared biological function. We apply the latent tree graphical model to a yeast stress response dataset. In addition to novel predictions, such as condition-specific binding of the transcription factor Msn4, our model recovers many known aspects of the yeast regulatory network. These include groups of co-regulated genes, condition-specific regulator activity, and combinatorial regulation among transcription factors. The latent tree graphical model is a general approach for analyzing gene expression data that requires no prior knowledge of which possible regulators exist, regulator activity, or where transcription factors physically bind.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge