Unsupervised Learning of Hybrid Latent Dynamics: A Learn-to-Identify Framework
Paper and Code
Mar 13, 2024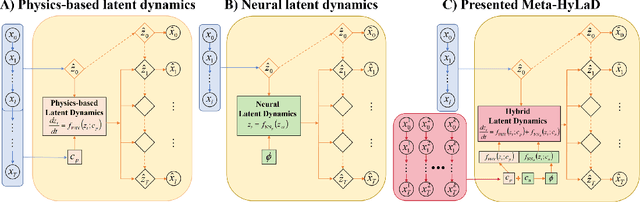
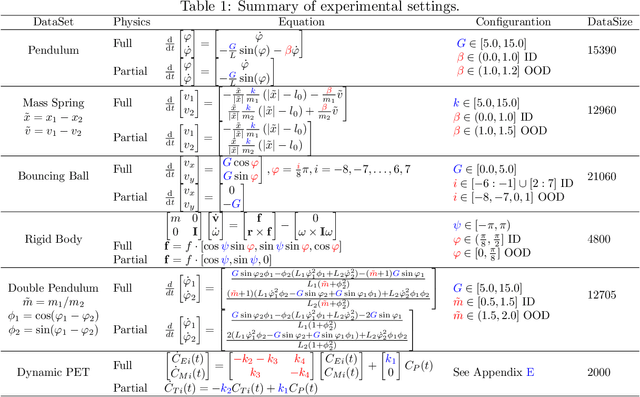
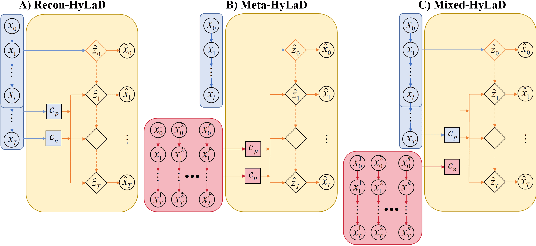

Modern applications increasingly require unsupervised learning of latent dynamics from high-dimensional time-series. This presents a significant challenge of identifiability: many abstract latent representations may reconstruct observations, yet do they guarantee an adequate identification of the governing dynamics? This paper investigates this challenge from two angles: the use of physics inductive bias specific to the data being modeled, and a learn-to-identify strategy that separates forecasting objectives from the data used for the identification. We combine these two strategies in a novel framework for unsupervised meta-learning of hybrid latent dynamics (Meta-HyLaD) with: 1) a latent dynamic function that hybridize known mathematical expressions of prior physics with neural functions describing its unknown errors, and 2) a meta-learning formulation to learn to separately identify both components of the hybrid dynamics. Through extensive experiments on five physics and one biomedical systems, we provide strong evidence for the benefits of Meta-HyLaD to integrate rich prior knowledge while identifying their gap to observed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge