Unit Selection: Learning Benefit Function from Finite Population Data
Paper and Code
Oct 15, 2022
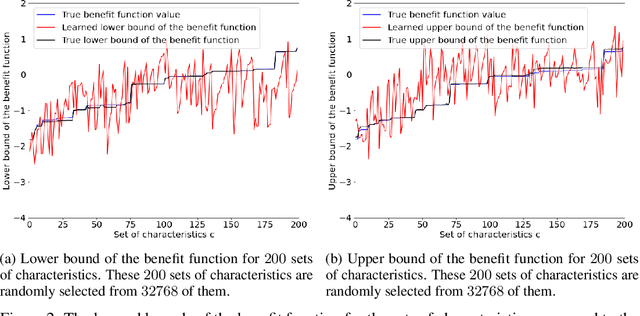
The unit selection problem is to identify a group of individuals who are most likely to exhibit a desired mode of behavior, for example, selecting individuals who would respond one way if incentivized and a different way if not. The unit selection problem consists of evaluation and search subproblems. Li and Pearl defined the "benefit function" to evaluate the average payoff of selecting a certain individual with given characteristics. The search subproblem is then to design an algorithm to identify the characteristics that maximize the above benefit function. The hardness of the search subproblem arises due to the large number of characteristics available for each individual and the sparsity of the data available in each cell of characteristics. In this paper, we present a machine learning framework that uses the bounds of the benefit function that are estimable from the finite population data to learn the bounds of the benefit function for each cell of characteristics. Therefore, we could easily obtain the characteristics that maximize the benefit function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge