Unique sparse decomposition of low rank matrices
Paper and Code
Jun 14, 2021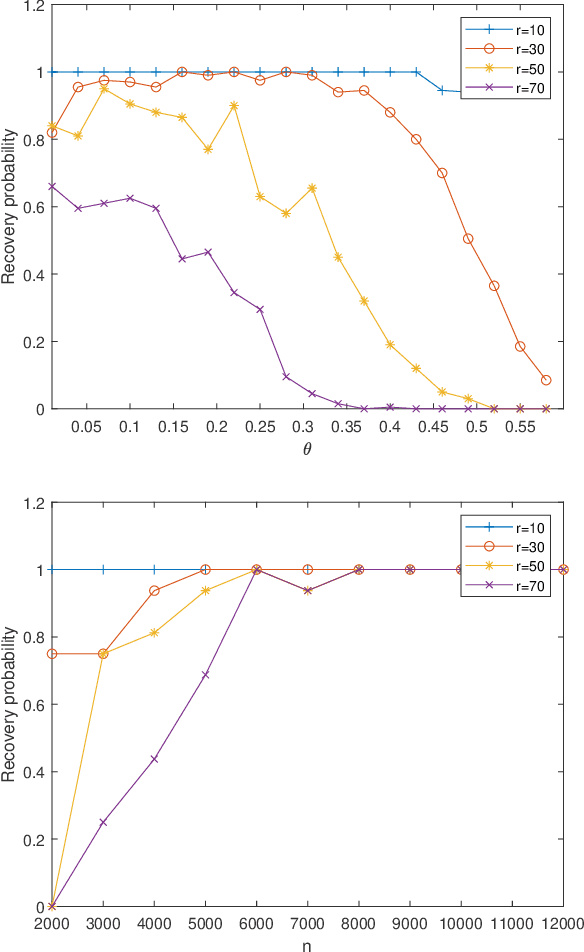
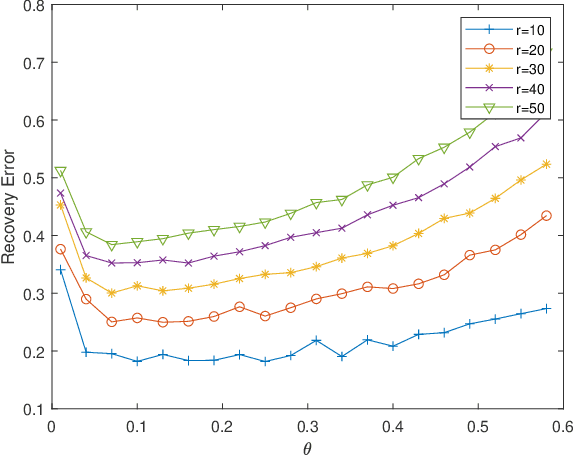
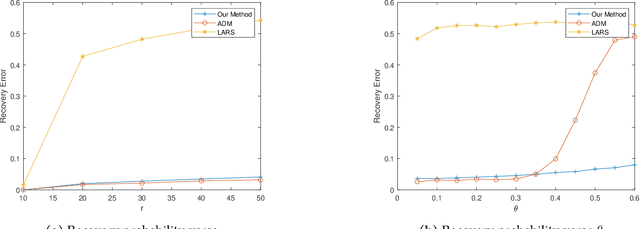
The problem of finding the unique low dimensional decomposition of a given matrix has been a fundamental and recurrent problem in many areas. In this paper, we study the problem of seeking a unique decomposition of a low rank matrix $Y\in \mathbb{R}^{p\times n}$ that admits a sparse representation. Specifically, we consider $Y = A X\in \mathbb{R}^{p\times n}$ where the matrix $A\in \mathbb{R}^{p\times r}$ has full column rank, with $r < \min\{n,p\}$, and the matrix $X\in \mathbb{R}^{r\times n}$ is element-wise sparse. We prove that this sparse decomposition of $Y$ can be uniquely identified, up to some intrinsic signed permutation. Our approach relies on solving a nonconvex optimization problem constrained over the unit sphere. Our geometric analysis for the nonconvex optimization landscape shows that any {\em strict} local solution is close to the ground truth solution, and can be recovered by a simple data-driven initialization followed with any second order descent algorithm. At last, we corroborate these theoretical results with numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge