Understanding and Mitigating Accuracy Disparity in Regression
Paper and Code
Feb 24, 2021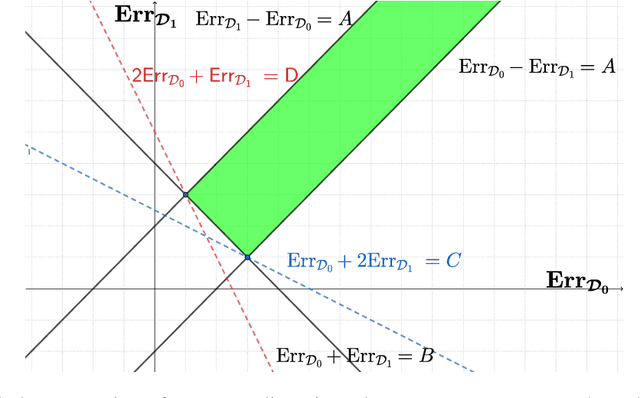

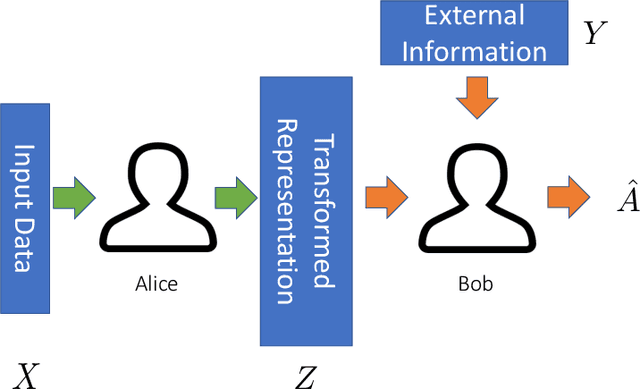
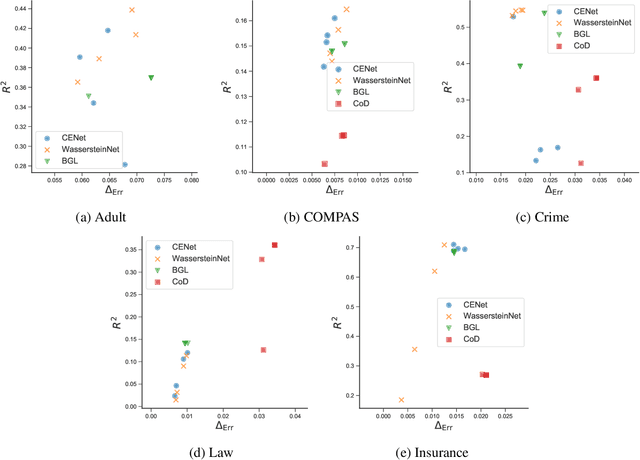
With the widespread deployment of large-scale prediction systems in high-stakes domains, e.g., face recognition, criminal justice, etc., disparity on prediction accuracy between different demographic subgroups has called for fundamental understanding on the source of such disparity and algorithmic intervention to mitigate it. In this paper, we study the accuracy disparity problem in regression. To begin with, we first propose an error decomposition theorem, which decomposes the accuracy disparity into the distance between marginal label distributions and the distance between conditional representations, to help explain why such accuracy disparity appears in practice. Motivated by this error decomposition and the general idea of distribution alignment with statistical distances, we then propose an algorithm to reduce this disparity, and analyze its game-theoretic optima of the proposed objective functions. To corroborate our theoretical findings, we also conduct experiments on five benchmark datasets. The experimental results suggest that our proposed algorithms can effectively mitigate accuracy disparity while maintaining the predictive power of the regression models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge