Uncertainty Quantification for Hyperspectral Image Denoising Frameworks based on Low-rank Matrix Approximation

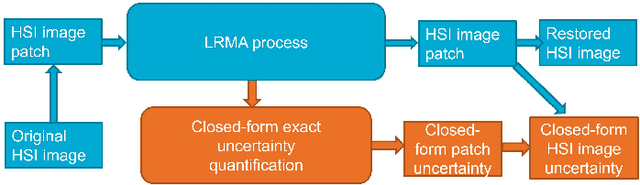
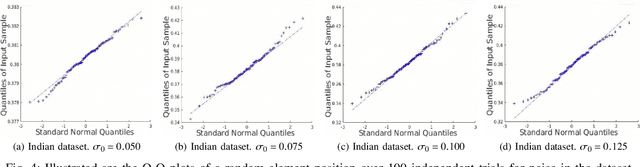
Low-rank matrix approximation (LRMA) is a technique widely applied in hyperspectral images (HSI) denoising or completion. The uncertainty quantification of the estimated restored HSI, however, has not been addressed in previous researches. The lack of uncertainty of the product significantly limits the applications like multi-source or multi-scale data fusion, data assimilation and product confidence quantification, since these applications require an accurate way to describe the statistical distributions of the source data. To address this issue, we propose a prior-free closed-form element-wise uncertainty quantification method for the LRMA based HSI restoration. The proposed approach only requires the uncertainty of the observed HSI and can yield uncertainty in a limited amount of time and with similar time complexity comparing to the LRMA technique. We conduct extensive experiments to validate that the closed-form uncertainty describes the estimation accurately, is robust to at least 10\% ratio of random impulse noises and takes only around 10-20% amount of time of LRMA. All the experiments indicate that the proposed closed-form uncertainty quantification method is more applicable to be deployed to real-world applications than the baseline Monte-Carlo tests.