Uncertainty Estimates for Ordinal Embeddings
Paper and Code
Jun 27, 2019
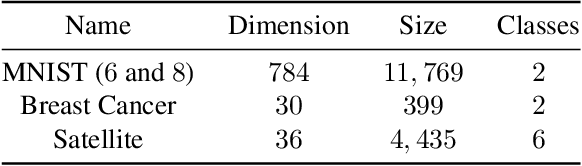


To investigate objects without a describable notion of distance, one can gather ordinal information by asking triplet comparisons of the form "Is object $x$ closer to $y$ or is $x$ closer to $z$?" In order to learn from such data, the objects are typically embedded in a Euclidean space while satisfying as many triplet comparisons as possible. In this paper, we introduce empirical uncertainty estimates for standard embedding algorithms when few noisy triplets are available, using a bootstrap and a Bayesian approach. In particular, simulations show that these estimates are well calibrated and can serve to select embedding parameters or to quantify uncertainty in scientific applications.
* 16 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge