Uncertainty Decomposition in Bayesian Neural Networks with Latent Variables
Paper and Code
Nov 11, 2017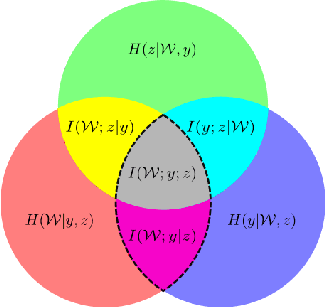
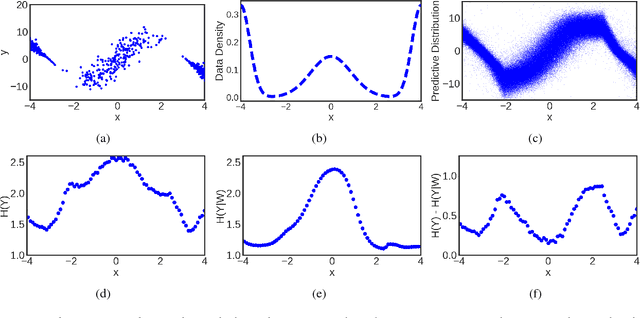
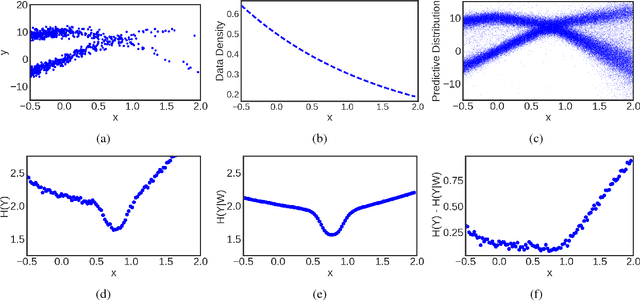
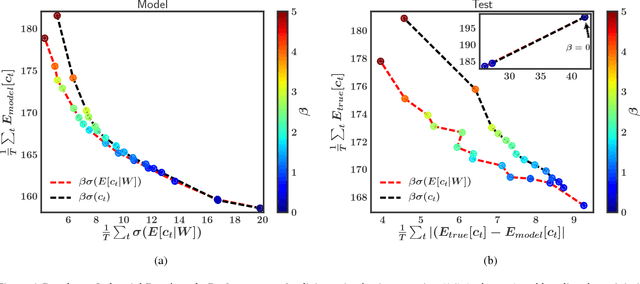
Bayesian neural networks (BNNs) with latent variables are probabilistic models which can automatically identify complex stochastic patterns in the data. We describe and study in these models a decomposition of predictive uncertainty into its epistemic and aleatoric components. First, we show how such a decomposition arises naturally in a Bayesian active learning scenario by following an information theoretic approach. Second, we use a similar decomposition to develop a novel risk sensitive objective for safe reinforcement learning (RL). This objective minimizes the effect of model bias in environments whose stochastic dynamics are described by BNNs with latent variables. Our experiments illustrate the usefulness of the resulting decomposition in active learning and safe RL settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge