Uncertainty-Aware CNNs for Depth Completion: Uncertainty from Beginning to End
Paper and Code
Jun 05, 2020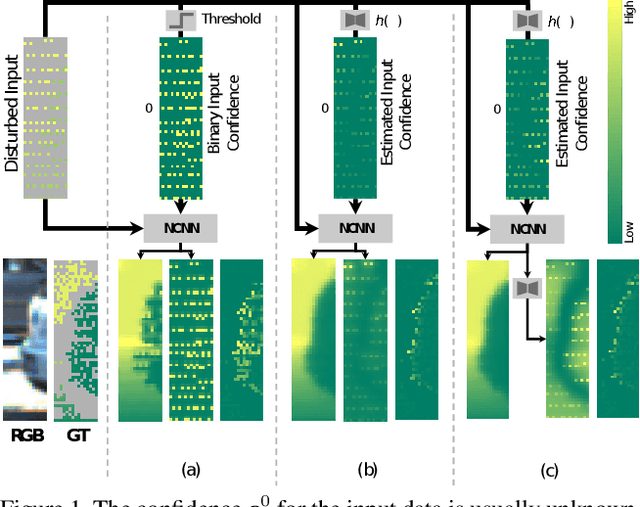
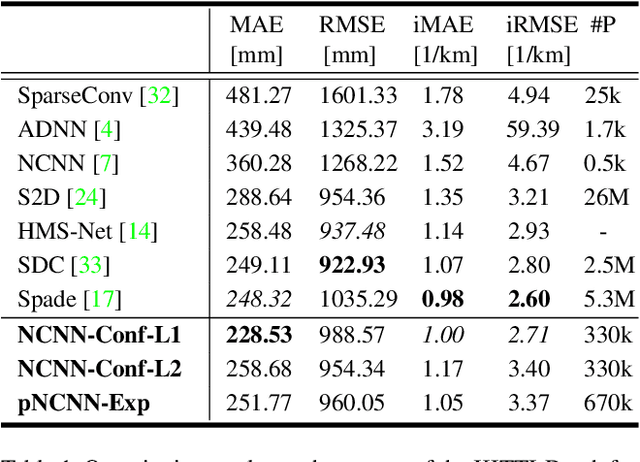
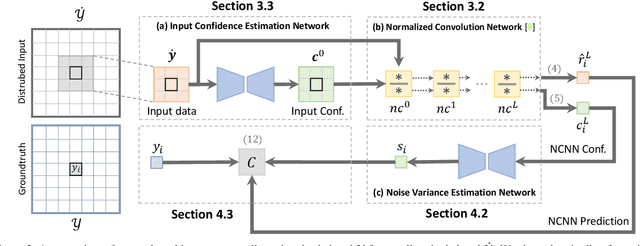
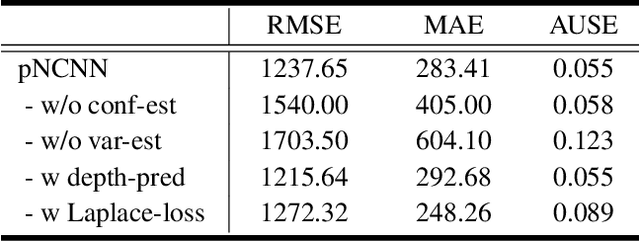
The focus in deep learning research has been mostly to push the limits of prediction accuracy. However, this was often achieved at the cost of increased complexity, raising concerns about the interpretability and the reliability of deep networks. Recently, an increasing attention has been given to untangling the complexity of deep networks and quantifying their uncertainty for different computer vision tasks. Differently, the task of depth completion has not received enough attention despite the inherent noisy nature of depth sensors. In this work, we thus focus on modeling the uncertainty of depth data in depth completion starting from the sparse noisy input all the way to the final prediction. We propose a novel approach to identify disturbed measurements in the input by learning an input confidence estimator in a self-supervised manner based on the normalized convolutional neural networks (NCNNs). Further, we propose a probabilistic version of NCNNs that produces a statistically meaningful uncertainty measure for the final prediction. When we evaluate our approach on the KITTI dataset for depth completion, we outperform all the existing Bayesian Deep Learning approaches in terms of prediction accuracy, quality of the uncertainty measure, and the computational efficiency. Moreover, our small network with 670k parameters performs on-par with conventional approaches with millions of parameters. These results give strong evidence that separating the network into parallel uncertainty and prediction streams leads to state-of-the-art performance with accurate uncertainty estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge