Uncertainty-Autoencoder-Based Privacy and Utility Preserving Data Type Conscious Transformation
Paper and Code
May 04, 2022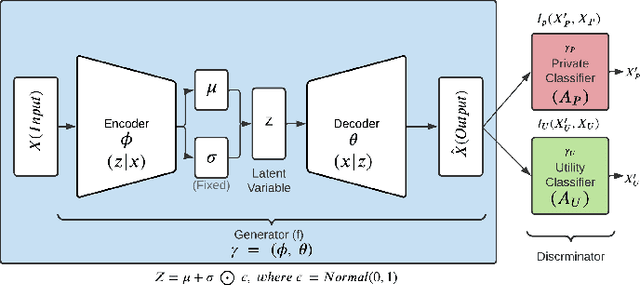
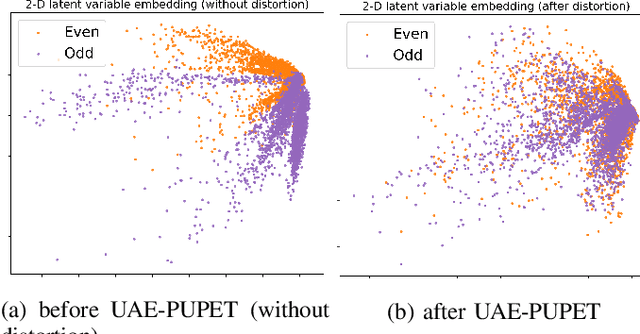
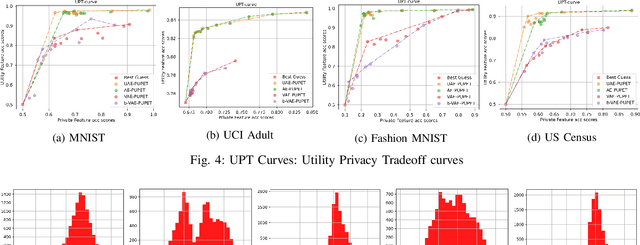

We propose an adversarial learning framework that deals with the privacy-utility tradeoff problem under two types of conditions: data-type ignorant, and data-type aware. Under data-type aware conditions, the privacy mechanism provides a one-hot encoding of categorical features, representing exactly one class, while under data-type ignorant conditions the categorical variables are represented by a collection of scores, one for each class. We use a neural network architecture consisting of a generator and a discriminator, where the generator consists of an encoder-decoder pair, and the discriminator consists of an adversary and a utility provider. Unlike previous research considering this kind of architecture, which leverages autoencoders (AEs) without introducing any randomness, or variational autoencoders (VAEs) based on learning latent representations which are then forced into a Gaussian assumption, our proposed technique introduces randomness and removes the Gaussian assumption restriction on the latent variables, only focusing on the end-to-end stochastic mapping of the input to privatized data. We test our framework on different datasets: MNIST, FashionMNIST, UCI Adult, and US Census Demographic Data, providing a wide range of possible private and utility attributes. We use multiple adversaries simultaneously to test our privacy mechanism -- some trained from the ground truth data and some trained from the perturbed data generated by our privacy mechanism. Through comparative analysis, our results demonstrate better privacy and utility guarantees than the existing works under similar, data-type ignorant conditions, even when the latter are considered under their original restrictive single-adversary model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge