Uncertain Pose Estimation during Contact Tasks using Differentiable Contact Features
Paper and Code
May 26, 2023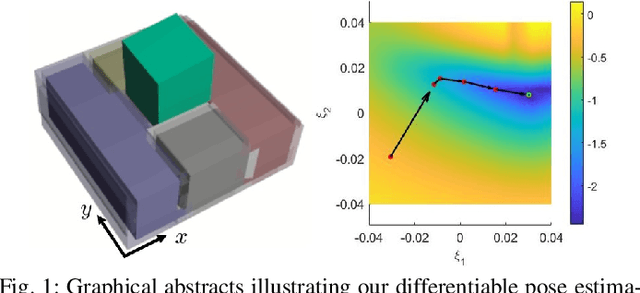
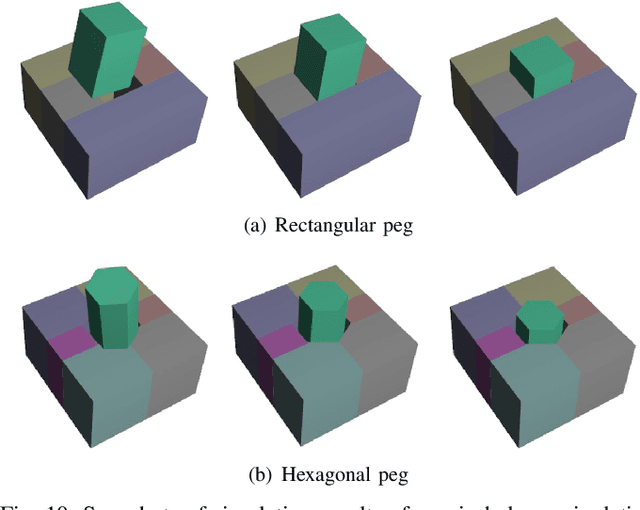
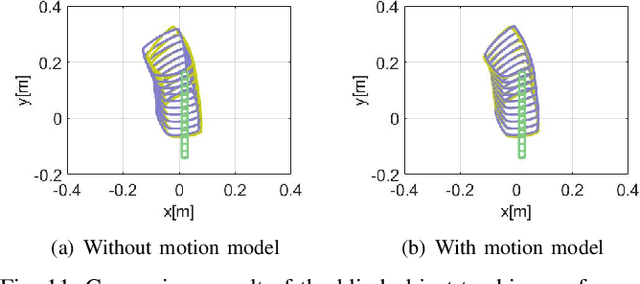

For many robotic manipulation and contact tasks, it is crucial to accurately estimate uncertain object poses, for which certain geometry and sensor information are fused in some optimal fashion. Previous results for this problem primarily adopt sampling-based or end-to-end learning methods, which yet often suffer from the issues of efficiency and generalizability. In this paper, we propose a novel differentiable framework for this uncertain pose estimation during contact, so that it can be solved in an efficient and accurate manner with gradient-based solver. To achieve this, we introduce a new geometric definition that is highly adaptable and capable of providing differentiable contact features. Then we approach the problem from a bi-level perspective and utilize the gradient of these contact features along with differentiable optimization to efficiently solve for the uncertain pose. Several scenarios are implemented to demonstrate how the proposed framework can improve existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge