Ultimate Power of Inference Attacks: Privacy Risks of High-Dimensional Models

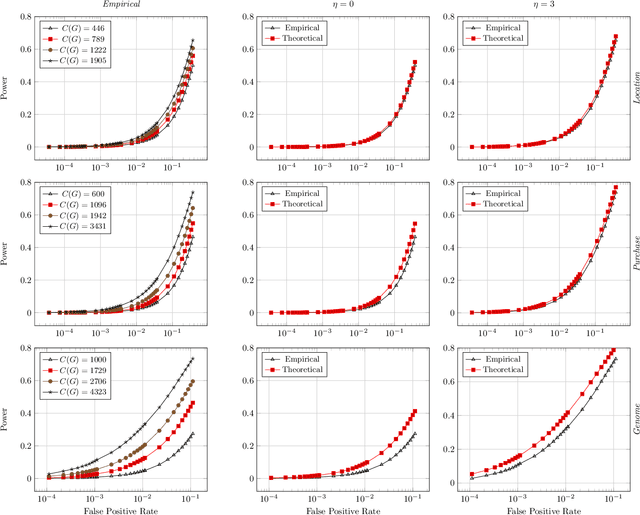
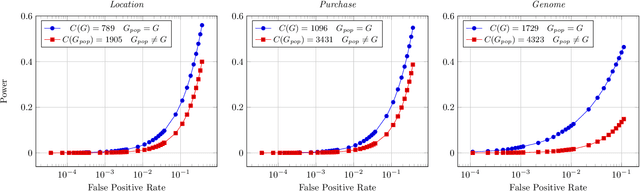
Models leak information about their training data. This enables attackers to infer sensitive information about their training sets, notably determine if a data sample was part of the model's training set. The existing works empirically show the possibility of these tracing (membership inference) attacks against complex models with a large number of parameters. However, the attack results are dependent on the specific training data, can be obtained only after the tedious process of training the model and performing the attack, and are missing any measure of the confidence and unused potential power of the attack. A model designer is interested in identifying which model structures leak more information, how adding new parameters to the model increases its privacy risk, and what is the gain of adding new data points to decrease the overall information leakage. The privacy analysis should also enable designing the most powerful inference attack. In this paper, we design a theoretical framework to analyze the maximum power of tracing attacks against high-dimensional models, with the focus on probabilistic graphical models. We provide a tight upper-bound on the power (true positive rate) of these attacks, with respect to their error (false positive rate). The bound, as it should be, is independent of the knowledge and algorithm of any specific attack, as well as the values of particular samples in the training set. It provides a measure of the potential leakage of a model given its structure, as a function of the structure complexity and the size of training set.