Two Sides of the Same Coin: Heterophily and Oversmoothing in Graph Convolutional Neural Networks

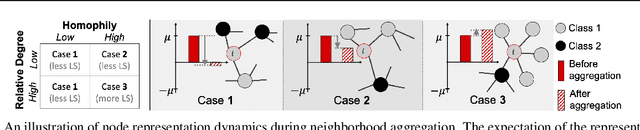
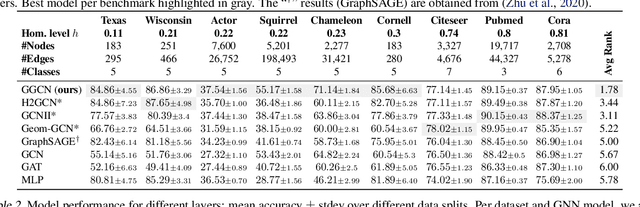
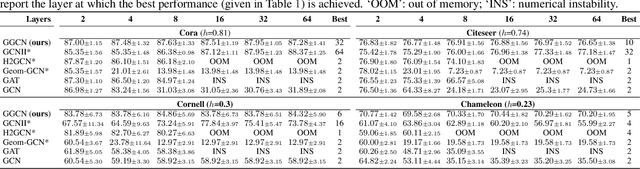
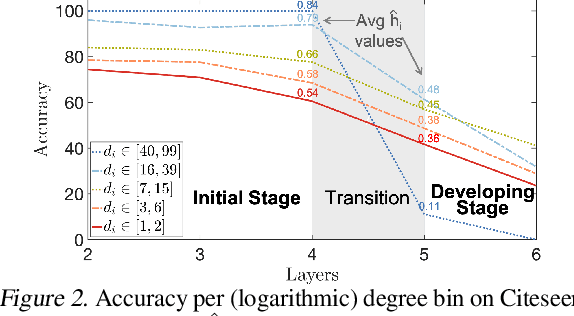
Most graph neural networks (GNN) perform poorly in graphs where neighbors typically have different features/classes (heterophily) and when stacking multiple layers (oversmoothing). These two seemingly unrelated problems have been studied independently, but there is recent empirical evidence that solving one problem may benefit the other. In this work, going beyond empirical observations, we theoretically characterize the connections between heterophily and oversmoothing, both of which lead to indistinguishable node representations. By modeling the change in node representations during message propagation, we theoretically analyze the factors (e.g., degree, heterophily level) that make the representations of nodes from different classes indistinguishable. Our analysis highlights that (1) nodes with high heterophily and nodes with low heterophily and low degrees relative to their neighbors (degree discrepancy) trigger the oversmoothing problem, and (2) allowing "negative" messages between neighbors can decouple the heterophily and oversmoothing problems. Based on our insights, we design a model that addresses the discrepancy in features and degrees between neighbors by incorporating signed messages and learned degree corrections. Our experiments on 9 real networks show that our model achieves state-of-the-art performance under heterophily, and performs comparably to existing GNNs under low heterophily(homophily). It also effectively addresses oversmoothing and even benefits from multiple layers.