Two-sided fairness in rankings via Lorenz dominance
Paper and Code
Oct 28, 2021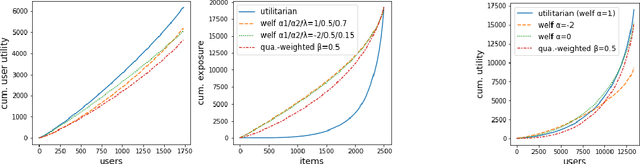

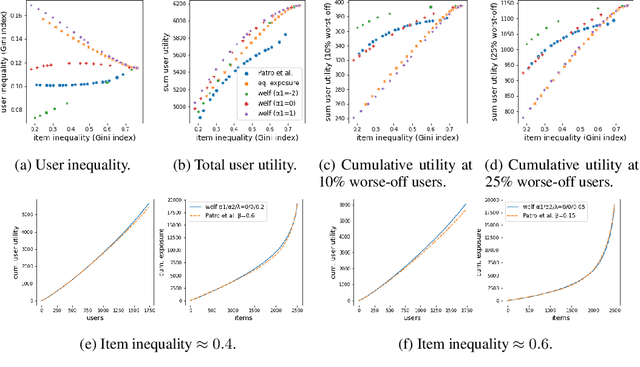

We consider the problem of generating rankings that are fair towards both users and item producers in recommender systems. We address both usual recommendation (e.g., of music or movies) and reciprocal recommendation (e.g., dating). Following concepts of distributive justice in welfare economics, our notion of fairness aims at increasing the utility of the worse-off individuals, which we formalize using the criterion of Lorenz efficiency. It guarantees that rankings are Pareto efficient, and that they maximally redistribute utility from better-off to worse-off, at a given level of overall utility. We propose to generate rankings by maximizing concave welfare functions, and develop an efficient inference procedure based on the Frank-Wolfe algorithm. We prove that unlike existing approaches based on fairness constraints, our approach always produces fair rankings. Our experiments also show that it increases the utility of the worse-off at lower costs in terms of overall utility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge