Tuning Confidence Bound for Stochastic Bandits with Bandit Distance
Paper and Code
Oct 06, 2021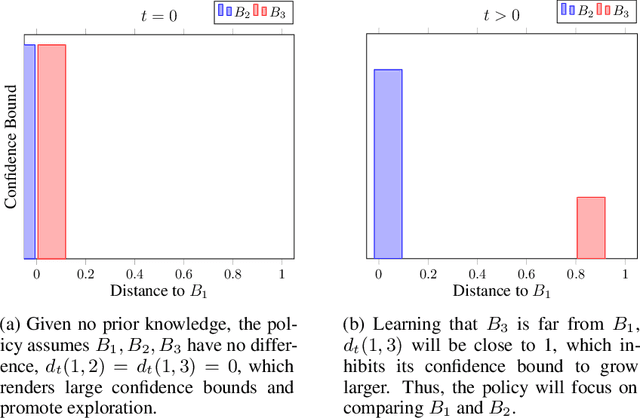
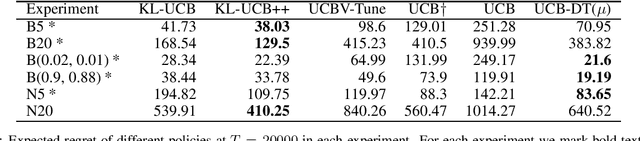
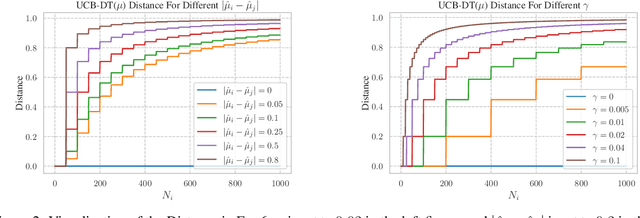

We propose a novel modification of the standard upper confidence bound (UCB) method for the stochastic multi-armed bandit (MAB) problem which tunes the confidence bound of a given bandit based on its distance to others. Our UCB distance tuning (UCB-DT) formulation enables improved performance as measured by expected regret by preventing the MAB algorithm from focusing on non-optimal bandits which is a well-known deficiency of standard UCB. "Distance tuning" of the standard UCB is done using a proposed distance measure, which we call bandit distance, that is parameterizable and which therefore can be optimized to control the transition rate from exploration to exploitation based on problem requirements. We empirically demonstrate increased performance of UCB-DT versus many existing state-of-the-art methods which use the UCB formulation for the MAB problem. Our contribution also includes the development of a conceptual tool called the "Exploration Bargain Point" which gives insights into the tradeoffs between exploration and exploitation. We argue that the Exploration Bargain Point provides an intuitive perspective that is useful for comparatively analyzing the performance of UCB-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge