Transient Performance Analysis of the $\ell_1$-RLS
Paper and Code
Sep 14, 2021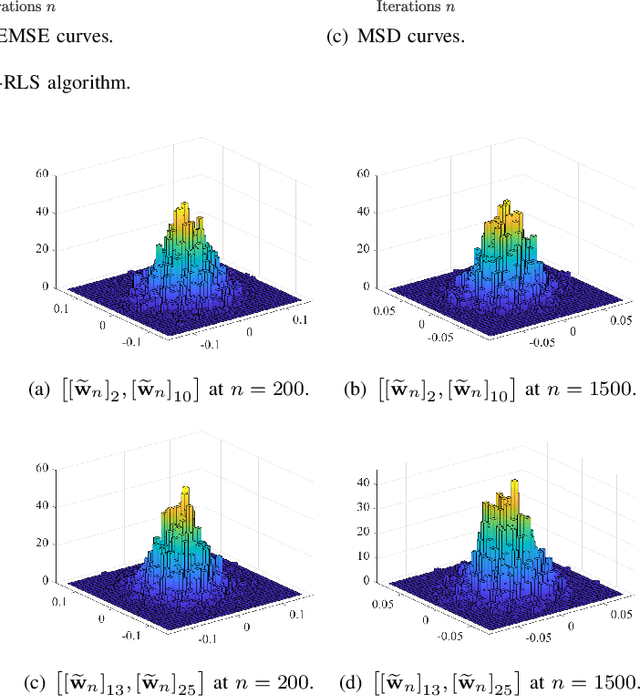
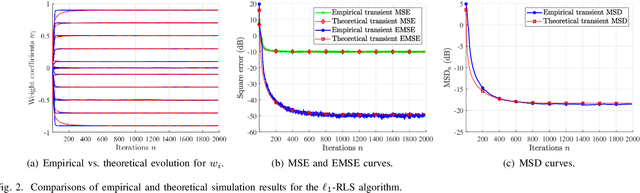
The recursive least-squares algorithm with $\ell_1$-norm regularization ($\ell_1$-RLS) exhibits excellent performance in terms of convergence rate and steady-state error in identification of sparse systems. Nevertheless few works have studied its stochastic behavior, in particular its transient performance. In this letter, we derive analytical models of the transient behavior of the $\ell_1$-RLS in the mean and mean-square sense. Simulation results illustrate the accuracy of these models.
* 5 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge