Transformers are Expressive, But Are They Expressive Enough for Regression?
Paper and Code
Feb 23, 2024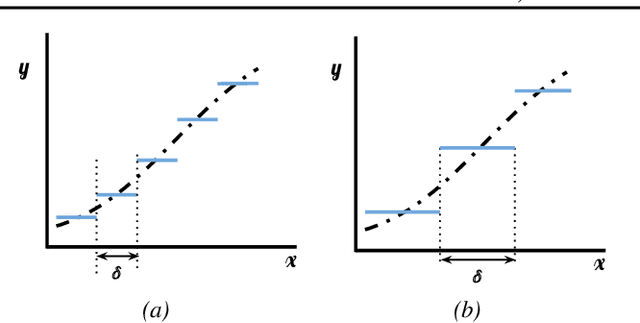

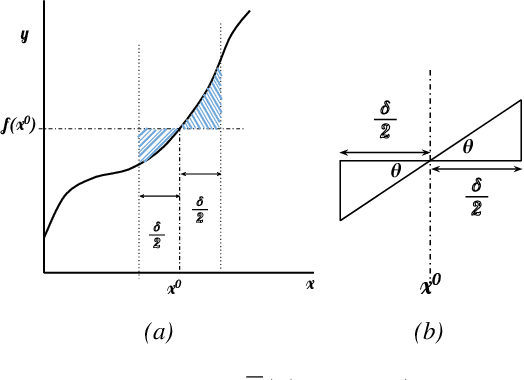

Transformers have become pivotal in Natural Language Processing, demonstrating remarkable success in applications like Machine Translation and Summarization. Given their widespread adoption, several works have attempted to analyze the expressivity of Transformers. Expressivity of a neural network is the class of functions it can approximate. A neural network is fully expressive if it can act as a universal function approximator. We attempt to analyze the same for Transformers. Contrary to existing claims, our findings reveal that Transformers struggle to reliably approximate continuous functions, relying on piecewise constant approximations with sizable intervals. The central question emerges as: "\textit{Are Transformers truly Universal Function Approximators}?" To address this, we conduct a thorough investigation, providing theoretical insights and supporting evidence through experiments. Our contributions include a theoretical analysis pinpointing the root of Transformers' limitation in function approximation and extensive experiments to verify the limitation. By shedding light on these challenges, we advocate a refined understanding of Transformers' capabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge