Transformations between deep neural networks

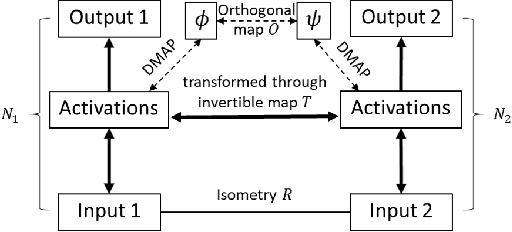
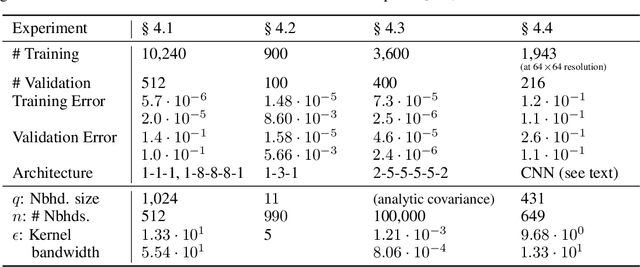
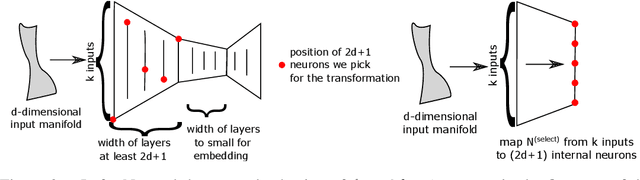
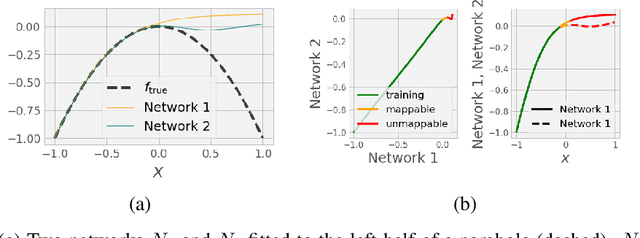
We propose to test, and when possible establish, an equivalence between two different artificial neural networks by attempting to construct a data-driven transformation between them, using manifold-learning techniques. In particular, we employ diffusion maps with a Mahalanobis-like metric. If the construction succeeds, the two networks can be thought of as belonging to the same equivalence class. We first discuss transformation functions between only the outputs of the two networks; we then also consider transformations that take into account outputs (activations) of a number of internal neurons from each network. In general, Whitney's theorem dictates the number of measurements from one of the networks required to reconstruct each and every feature of the second network. The construction of the transformation function relies on a consistent, intrinsic representation of the network input space. We illustrate our algorithm by matching neural network pairs trained to learn (a) observations of scalar functions; (b) observations of two-dimensional vector fields; and (c) representations of images of a moving three-dimensional object (a rotating horse). The construction of such equivalence classes across different network instantiations clearly relates to transfer learning. We also expect that it will be valuable in establishing equivalence between different Machine Learning-based models of the same phenomenon observed through different instruments and by different research groups.