Training β-VAE by Aggregating a Learned Gaussian Posterior with a Decoupled Decoder

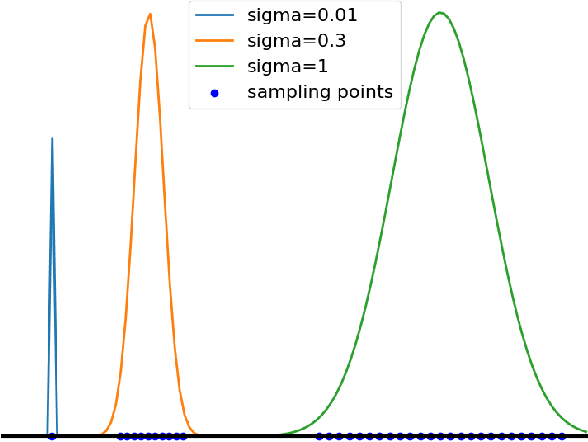
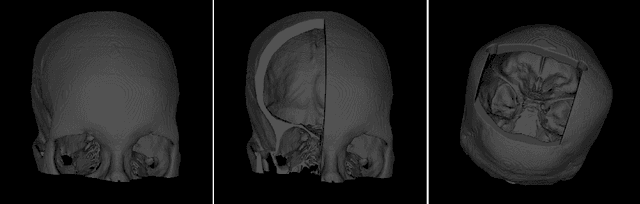
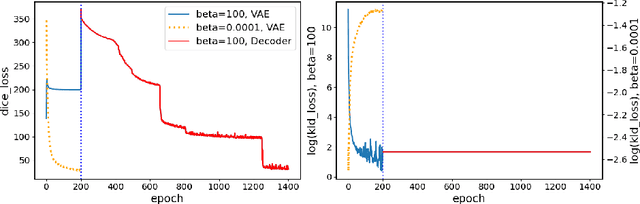
The reconstruction loss and the Kullback-Leibler divergence (KLD) loss in a variational autoencoder (VAE) often play antagonistic roles, and tuning the weight of the KLD loss in $\beta$-VAE to achieve a balance between the two losses is a tricky and dataset-specific task. As a result, current practices in VAE training often result in a trade-off between the reconstruction fidelity and the continuity$/$disentanglement of the latent space, if the weight $\beta$ is not carefully tuned. In this paper, we present intuitions and a careful analysis of the antagonistic mechanism of the two losses, and propose, based on the insights, a simple yet effective two-stage method for training a VAE. Specifically, the method aggregates a learned Gaussian posterior $z \sim q_{\theta} (z|x)$ with a decoder decoupled from the KLD loss, which is trained to learn a new conditional distribution $p_{\phi} (x|z)$ of the input data $x$. Experimentally, we show that the aggregated VAE maximally satisfies the Gaussian assumption about the latent space, while still achieves a reconstruction error comparable to when the latent space is only loosely regularized by $\mathcal{N}(\mathbf{0},I)$. The proposed approach does not require hyperparameter (i.e., the KLD weight $\beta$) tuning given a specific dataset as required in common VAE training practices. We evaluate the method using a medical dataset intended for 3D skull reconstruction and shape completion, and the results indicate promising generative capabilities of the VAE trained using the proposed method. Besides, through guided manipulation of the latent variables, we establish a connection between existing autoencoder (AE)-based approaches and generative approaches, such as VAE, for the shape completion problem. Codes and pre-trained weights are available at https://github.com/Jianningli/skullVAE