Training Binary Neural Networks using the Bayesian Learning Rule
Paper and Code
Mar 10, 2020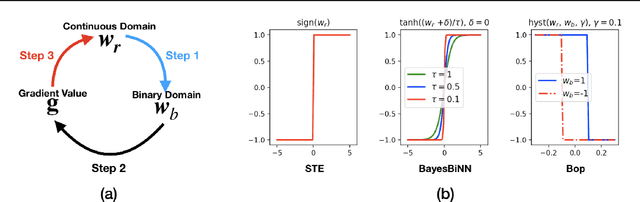

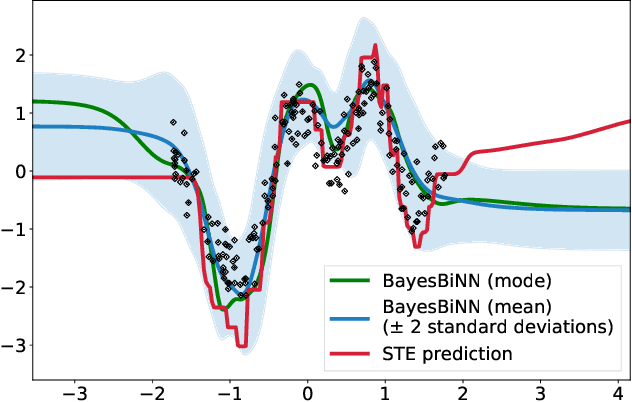
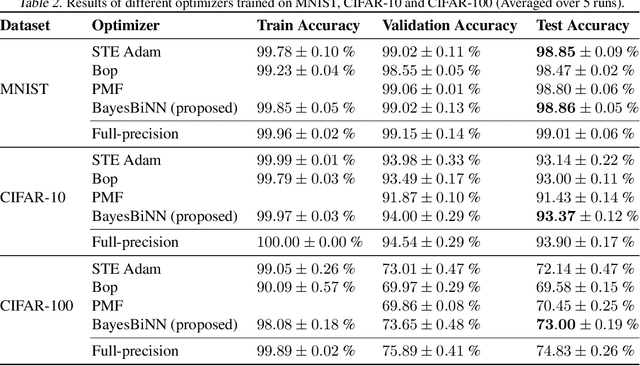
Neural networks with binary weights are computation-efficient and hardware-friendly, but their training is challenging because it involves a discrete optimization problem. Surprisingly, ignoring the discrete nature of the problem and using gradient-based methods, such as Straight-Through Estimator, still works well in practice. This raises the question: are there principled approaches which justify such methods? In this paper, we propose such an approach using the Bayesian learning rule. The rule, when applied to estimate a Bernoulli distribution over the binary weights, results in an algorithm which justifies some of the algorithmic choices made by the previous approaches. The algorithm not only obtains state-of-the-art performance, but also enables uncertainty estimation for continual learning to avoid catastrophic forgetting. Our work provides a principled approach for training binary neural networks which justifies and extends existing approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge