Towards the Identifiability in Noisy Label Learning: A Multinomial Mixture Approach

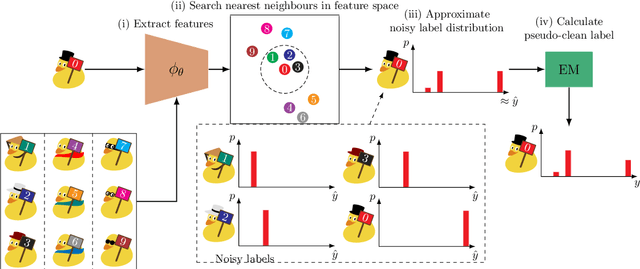
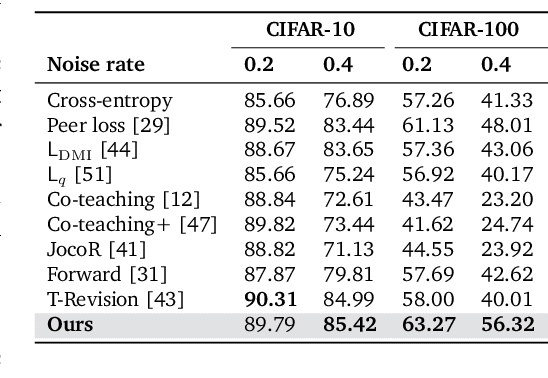
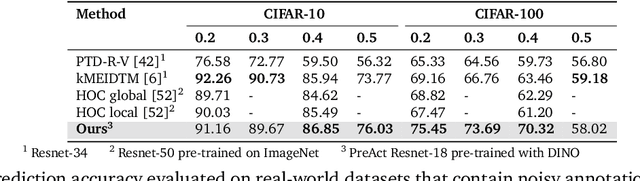
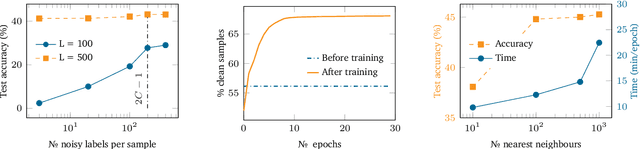
Learning from noisy labels plays an important role in the deep learning era. Despite numerous studies with promising results, identifying clean labels from a noisily-annotated dataset is still challenging since the conventional noisy label learning problem with single noisy label per instance is not identifiable, i.e., it does not theoretically have a unique solution unless one has access to clean labels or introduces additional assumptions. This paper aims to formally investigate such identifiability issue by formulating the noisy label learning problem as a multinomial mixture model, enabling the formulation of the identifiability constraint. In particular, we prove that the noisy label learning problem is identifiable if there are at least $2C - 1$ noisy labels per instance provided, with $C$ being the number of classes. In light of such requirement, we propose a method that automatically generates additional noisy labels per training sample by estimating the noisy label distribution based on nearest neighbours. Such additional noisy labels allow us to apply the Expectation - Maximisation algorithm to estimate the posterior of clean labels. We empirically demonstrate that the proposed method is not only capable of estimating clean labels without any heuristics in several challenging label noise benchmarks, including synthetic, web-controlled and real-world label noises, but also of performing competitively with many state-of-the-art methods.