Towards Optimal Randomized Strategies in Adversarial Example Game
Paper and Code
Jun 29, 2023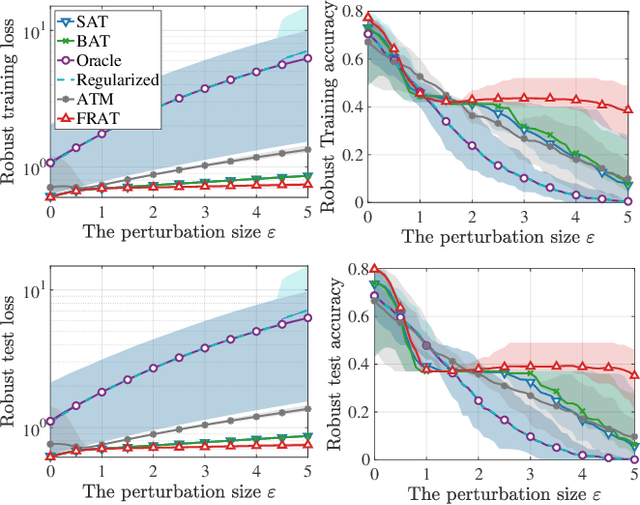
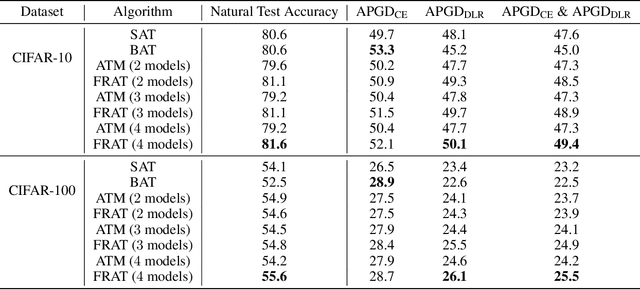
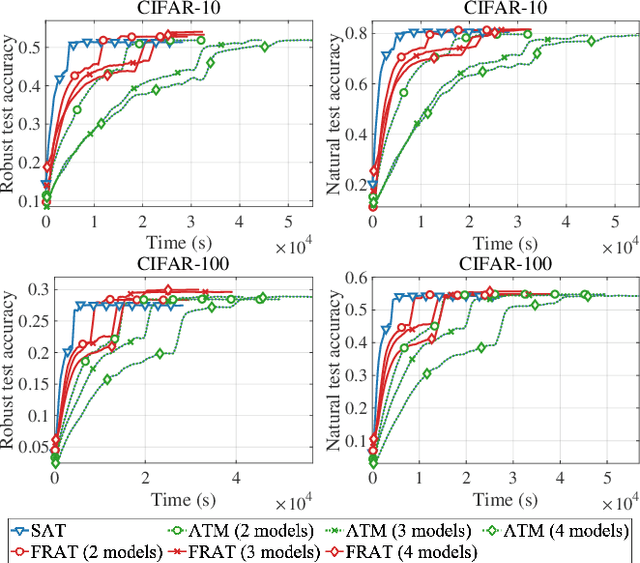
The vulnerability of deep neural network models to adversarial example attacks is a practical challenge in many artificial intelligence applications. A recent line of work shows that the use of randomization in adversarial training is the key to find optimal strategies against adversarial example attacks. However, in a fully randomized setting where both the defender and the attacker can use randomized strategies, there are no efficient algorithm for finding such an optimal strategy. To fill the gap, we propose the first algorithm of its kind, called FRAT, which models the problem with a new infinite-dimensional continuous-time flow on probability distribution spaces. FRAT maintains a lightweight mixture of models for the defender, with flexibility to efficiently update mixing weights and model parameters at each iteration. Furthermore, FRAT utilizes lightweight sampling subroutines to construct a random strategy for the attacker. We prove that the continuous-time limit of FRAT converges to a mixed Nash equilibria in a zero-sum game formed by a defender and an attacker. Experimental results also demonstrate the efficiency of FRAT on CIFAR-10 and CIFAR-100 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge