Totally Corrective Multiclass Boosting with Binary Weak Learners
Paper and Code
Sep 20, 2010
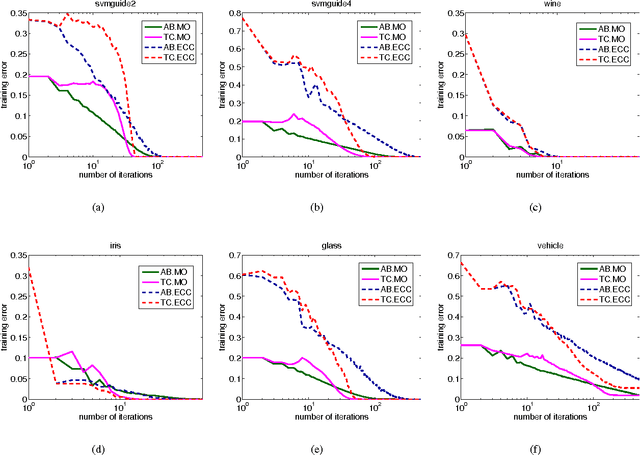
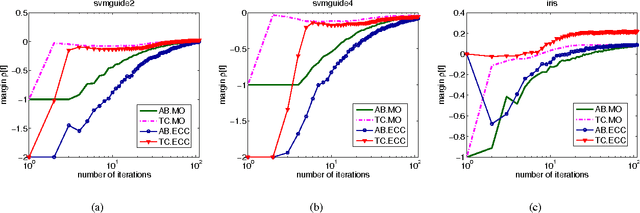
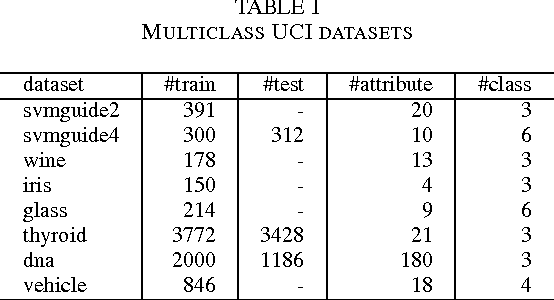
In this work, we propose a new optimization framework for multiclass boosting learning. In the literature, AdaBoost.MO and AdaBoost.ECC are the two successful multiclass boosting algorithms, which can use binary weak learners. We explicitly derive these two algorithms' Lagrange dual problems based on their regularized loss functions. We show that the Lagrange dual formulations enable us to design totally-corrective multiclass algorithms by using the primal-dual optimization technique. Experiments on benchmark data sets suggest that our multiclass boosting can achieve a comparable generalization capability with state-of-the-art, but the convergence speed is much faster than stage-wise gradient descent boosting. In other words, the new totally corrective algorithms can maximize the margin more aggressively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge