Total Least Squares Regression in Input Sparsity Time
Paper and Code
Sep 27, 2019
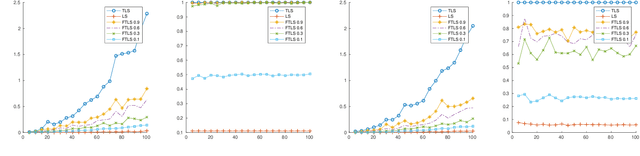
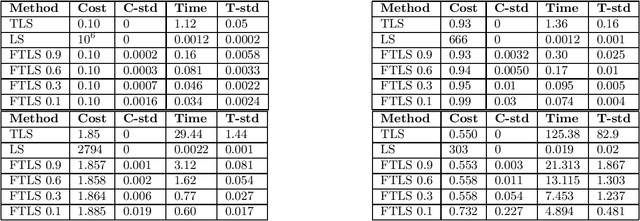
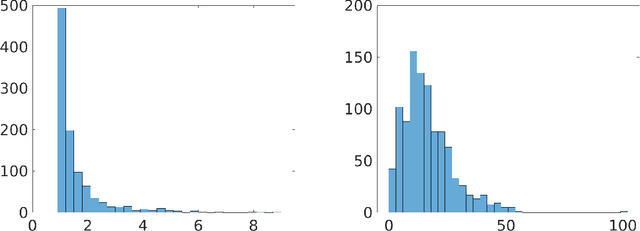
In the total least squares problem, one is given an $m \times n$ matrix $A$, and an $m \times d$ matrix $B$, and one seeks to "correct" both $A$ and $B$, obtaining matrices $\hat{A}$ and $\hat{B}$, so that there exists an $X$ satisfying the equation $\hat{A}X = \hat{B}$. Typically the problem is overconstrained, meaning that $m \gg \max(n,d)$. The cost of the solution $\hat{A}, \hat{B}$ is given by $\|A-\hat{A}\|_F^2 + \|B - \hat{B}\|_F^2$. We give an algorithm for finding a solution $X$ to the linear system $\hat{A}X=\hat{B}$ for which the cost $\|A-\hat{A}\|_F^2 + \|B-\hat{B}\|_F^2$ is at most a multiplicative $(1+\epsilon)$ factor times the optimal cost, up to an additive error $\eta$ that may be an arbitrarily small function of $n$. Importantly, our running time is $\tilde{O}( \mathrm{nnz}(A) + \mathrm{nnz}(B) ) + \mathrm{poly}(n/\epsilon) \cdot d$, where for a matrix $C$, $\mathrm{nnz}(C)$ denotes its number of non-zero entries. Importantly, our running time does not directly depend on the large parameter $m$. As total least squares regression is known to be solvable via low rank approximation, a natural approach is to invoke fast algorithms for approximate low rank approximation, obtaining matrices $\hat{A}$ and $\hat{B}$ from this low rank approximation, and then solving for $X$ so that $\hat{A}X = \hat{B}$. However, existing algorithms do not apply since in total least squares the rank of the low rank approximation needs to be $n$, and so the running time of known methods would be at least $mn^2$. In contrast, we are able to achieve a much faster running time for finding $X$ by never explicitly forming the equation $\hat{A} X = \hat{B}$, but instead solving for an $X$ which is a solution to an implicit such equation. Finally, we generalize our algorithm to the total least squares problem with regularization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge