Topological Gradient-based Competitive Learning
Paper and Code
Aug 21, 2020

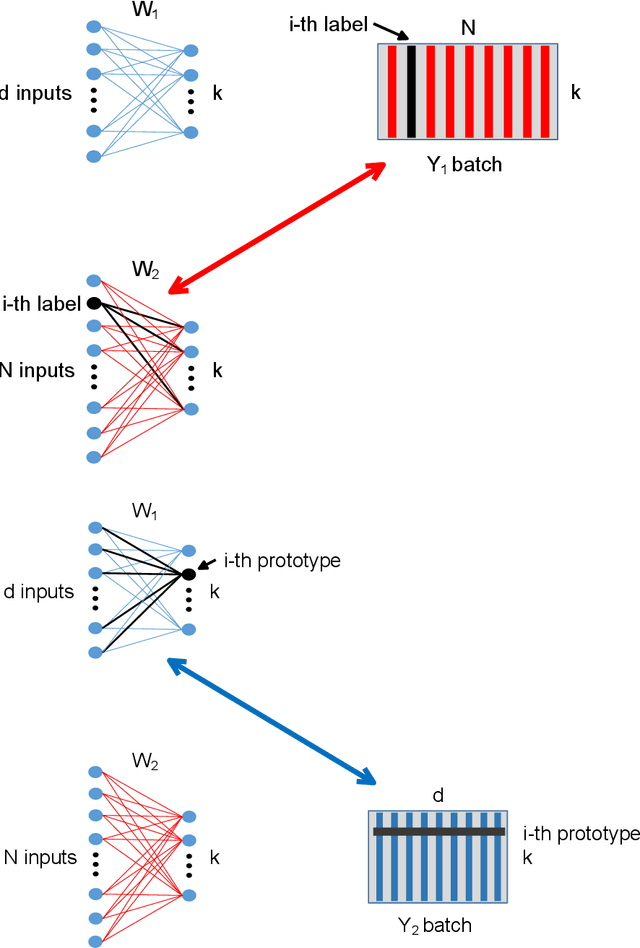
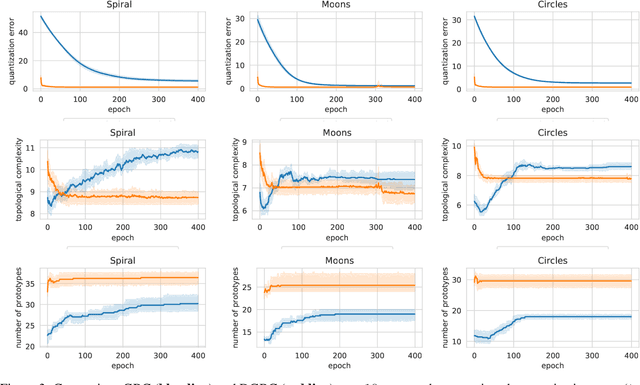
Topological learning is a wide research area aiming at uncovering the mutual spatial relationships between the elements of a set. Some of the most common and oldest approaches involve the use of unsupervised competitive neural networks. However, these methods are not based on gradient optimization which has been proven to provide striking results in feature extraction also in unsupervised learning. Unfortunately, by focusing mostly on algorithmic efficiency and accuracy, deep clustering techniques are composed of overly complex feature extractors, while using trivial algorithms in their top layer. The aim of this work is to present a novel comprehensive theory aspiring at bridging competitive learning with gradient-based learning, thus allowing the use of extremely powerful deep neural networks for feature extraction and projection combined with the remarkable flexibility and expressiveness of competitive learning. In this paper we fully demonstrate the theoretical equivalence of two novel gradient-based competitive layers. Preliminary experiments show how the dual approach, trained on the transpose of the input matrix i.e. $X^T$, lead to faster convergence rate and higher training accuracy both in low and high-dimensional scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge