To do or not to do: cost-sensitive causal decision-making
Paper and Code
Jan 05, 2021
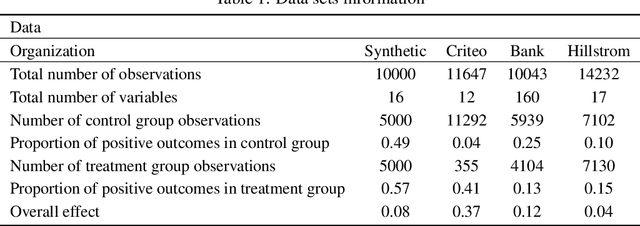

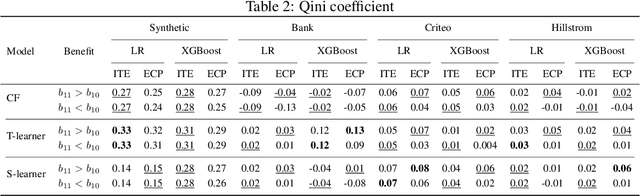
Causal classification models are adopted across a variety of operational business processes to predict the effect of a treatment on a categorical business outcome of interest depending on the process instance characteristics. This allows optimizing operational decision-making and selecting the optimal treatment to apply in each specific instance, with the aim of maximizing the positive outcome rate. While various powerful approaches have been presented in the literature for learning causal classification models, no formal framework has been elaborated for optimal decision-making based on the estimated individual treatment effects, given the cost of the various treatments and the benefit of the potential outcomes. In this article, we therefore extend upon the expected value framework and formally introduce a cost-sensitive decision boundary for double binary causal classification, which is a linear function of the estimated individual treatment effect, the positive outcome probability and the cost and benefit parameters of the problem setting. The boundary allows causally classifying instances in the positive and negative treatment class to maximize the expected causal profit, which is introduced as the objective at hand in cost-sensitive causal classification. We introduce the expected causal profit ranker which ranks instances for maximizing the expected causal profit at each possible threshold for causally classifying instances and differs from the conventional ranking approach based on the individual treatment effect. The proposed ranking approach is experimentally evaluated on synthetic and marketing campaign data sets. The results indicate that the presented ranking method effectively outperforms the cost-insensitive ranking approach and allows boosting profitability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge