Time-Delay Momentum: A Regularization Perspective on the Convergence and Generalization of Stochastic Momentum for Deep Learning

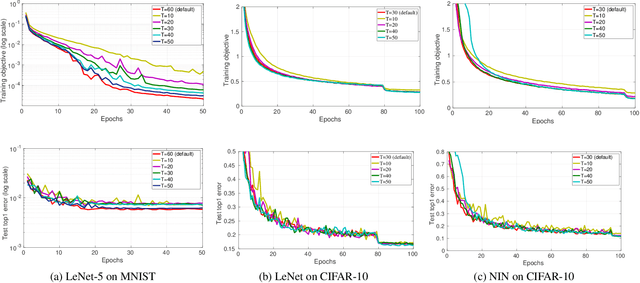
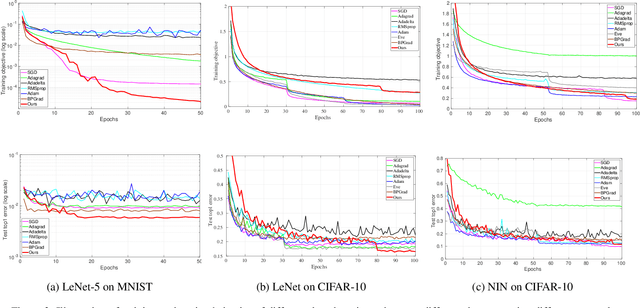
In this paper we study the problem of convergence and generalization error bound of stochastic momentum for deep learning from the perspective of regularization. To do so, we first interpret momentum as solving an $\ell_2$-regularized minimization problem to learn the offsets between arbitrary two successive model parameters. We call this {\em time-delay momentum} because the model parameter is updated after a few iterations towards finding the minimizer. We then propose our learning algorithm, \ie stochastic gradient descent (SGD) with time-delay momentum. We show that our algorithm can be interpreted as solving a sequence of strongly convex optimization problems using SGD. We prove that under mild conditions our algorithm can converge to a stationary point with rate of $O(\frac{1}{\sqrt{K}})$ and generalization error bound of $O(\frac{1}{\sqrt{n\delta}})$ with probability at least $1-\delta$, where $K,n$ are the numbers of model updates and training samples, respectively. We demonstrate the empirical superiority of our algorithm in deep learning in comparison with the state-of-the-art deep learning solvers.