Thresholded Adaptive Validation: Tuning the Graphical Lasso for Graph Recovery
Paper and Code
May 01, 2020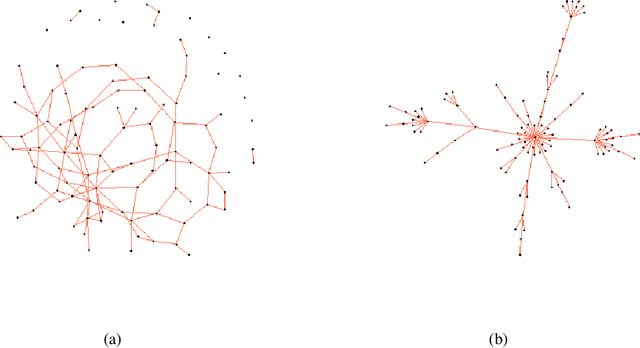
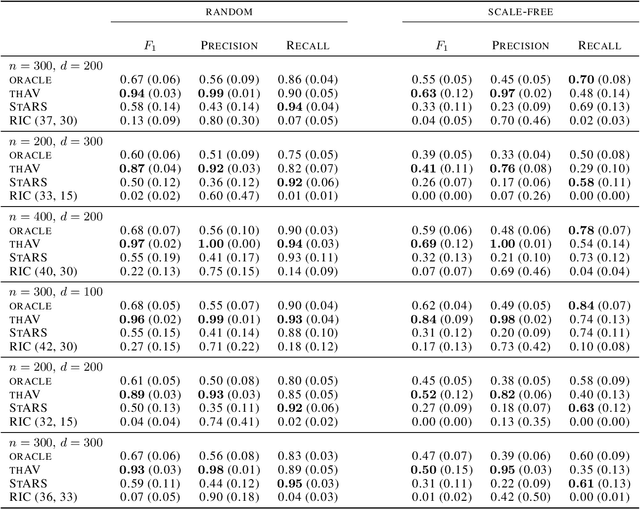
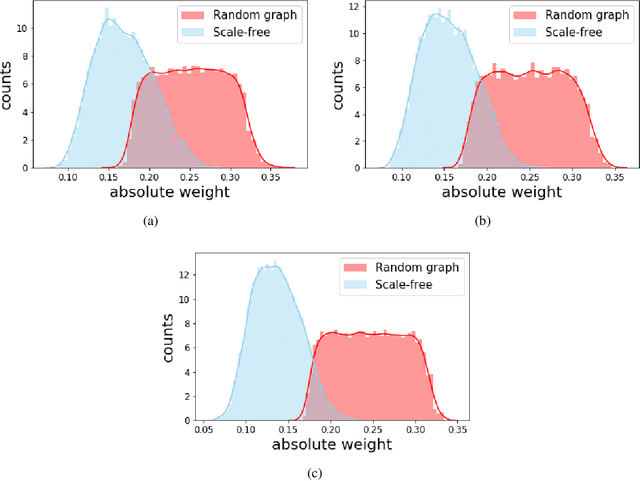
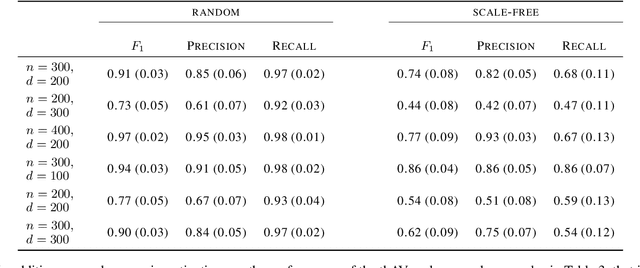
The graphical lasso is the most popular estimator in Gaussian graphical models, but its performance hinges on a regularization parameter that needs to be calibrated to each application at hand. In this paper, we propose a novel calibration scheme for this parameter. The scheme is equipped with theoretical guarantees and motivates a thresholding pipeline that can improve graph recovery. Moreover, requiring at most one line search over the regularization path of the graphical lasso, the calibration scheme is computationally more efficient than competing schemes that are based on resampling. Finally, we show in simulations that our approach can improve on the graph recovery of other approaches considerably.
* 26 pages, 10 figures, 9 tables
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge