Three-quarter Sibling Regression for Denoising Observational Data
Paper and Code
Dec 31, 2020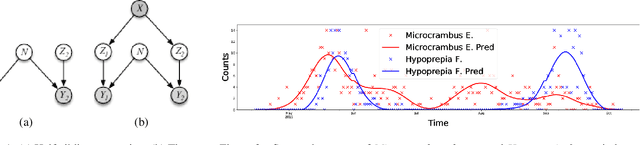
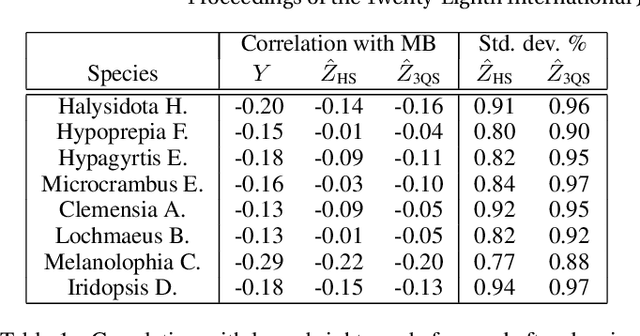
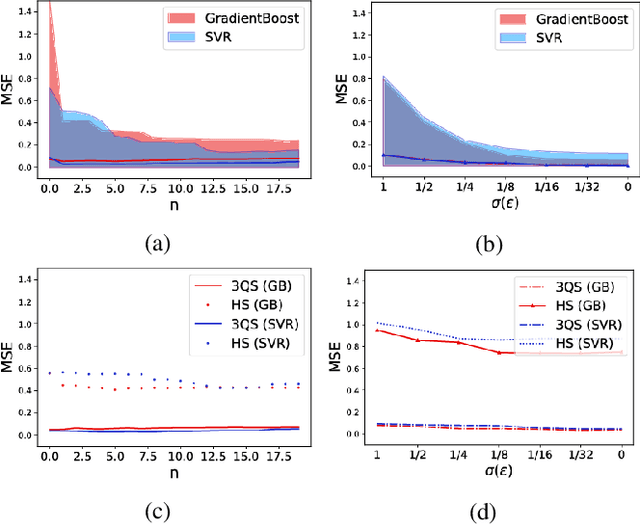
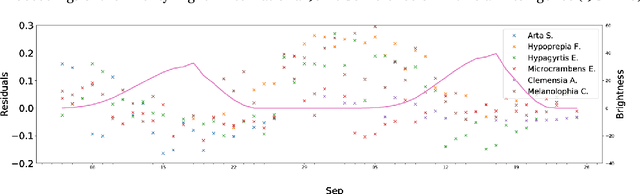
Many ecological studies and conservation policies are based on field observations of species, which can be affected by systematic variability introduced by the observation process. A recently introduced causal modeling technique called 'half-sibling regression' can detect and correct for systematic errors in measurements of multiple independent random variables. However, it will remove intrinsic variability if the variables are dependent, and therefore does not apply to many situations, including modeling of species counts that are controlled by common causes. We present a technique called 'three-quarter sibling regression' to partially overcome this limitation. It can filter the effect of systematic noise when the latent variables have observed common causes. We provide theoretical justification of this approach, demonstrate its effectiveness on synthetic data, and show that it reduces systematic detection variability due to moon brightness in moth surveys.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge