Thompson Sampling for Bandit Learning in Matching Markets
Paper and Code
May 02, 2022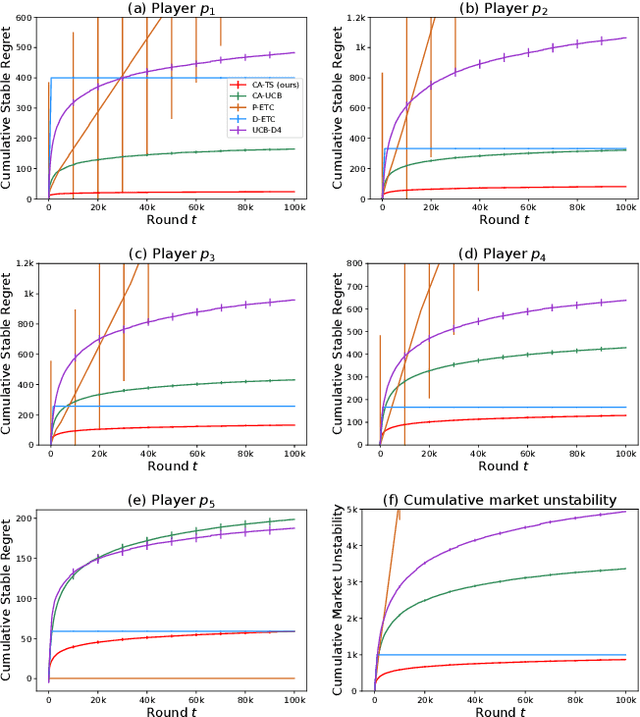
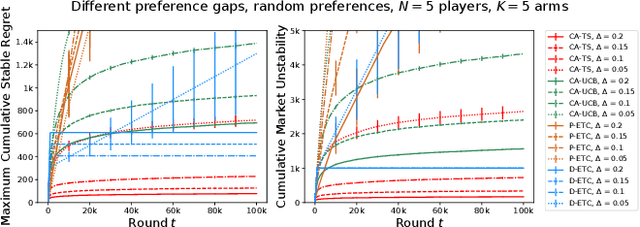
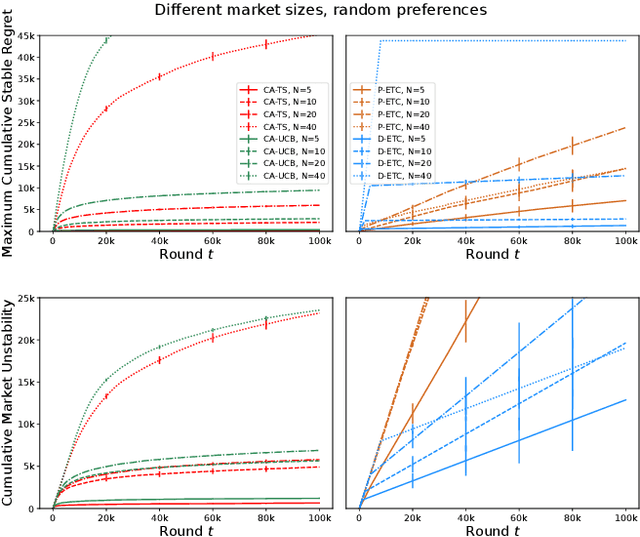
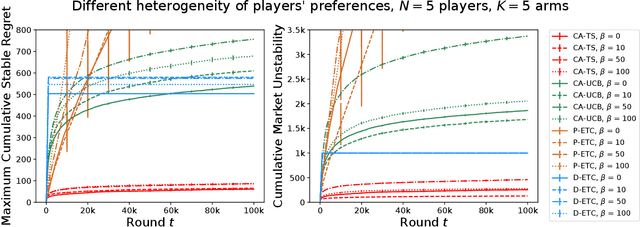
The problem of two-sided matching markets has a wide range of real-world applications and has been extensively studied in the literature. A line of recent works have focused on the problem setting where the preferences of one-side market participants are unknown \emph{a priori} and are learned by iteratively interacting with the other side of participants. All these works are based on explore-then-commit (ETC) and upper confidence bound (UCB) algorithms, two common strategies in multi-armed bandits (MAB). Thompson sampling (TS) is another popular approach, which attracts lots of attention due to its easier implementation and better empirical performances. In many problems, even when UCB and ETC-type algorithms have already been analyzed, researchers are still trying to study TS for its benefits. However, the convergence analysis of TS is much more challenging and remains open in many problem settings. In this paper, we provide the first regret analysis for TS in the new setting of iterative matching markets. Extensive experiments demonstrate the practical advantages of the TS-type algorithm over the ETC and UCB-type baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge