Theoretical Foundations of Hyperdimensional Computing

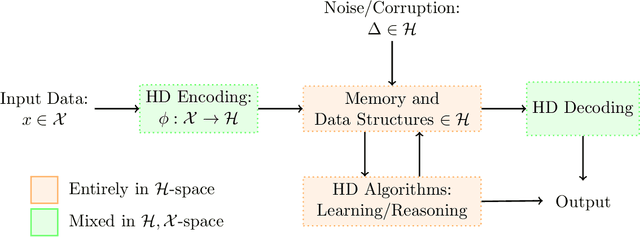
Hyperdimensional (HD) computing is a set of neurally inspired methods for obtaining high-dimensional, low-precision, distributed representations of data. These representations can be combined with simple, neurally plausible algorithms to effect a variety of information processing tasks. HD computing has recently garnered significant interest from the computer hardware community as an energy-efficient, low-latency, and noise robust tool for solving learning problems. In this work, we present a unified treatment of the theoretical foundations of HD computing with a focus on the suitability of representations for learning. In addition to providing a formal structure in which to study HD computing, we provide useful guidance for practitioners and lay out important open questions warranting further study.