Theoretical Analysis of Primal-Dual Algorithm for Non-Convex Stochastic Decentralized Optimization
Paper and Code
May 23, 2022
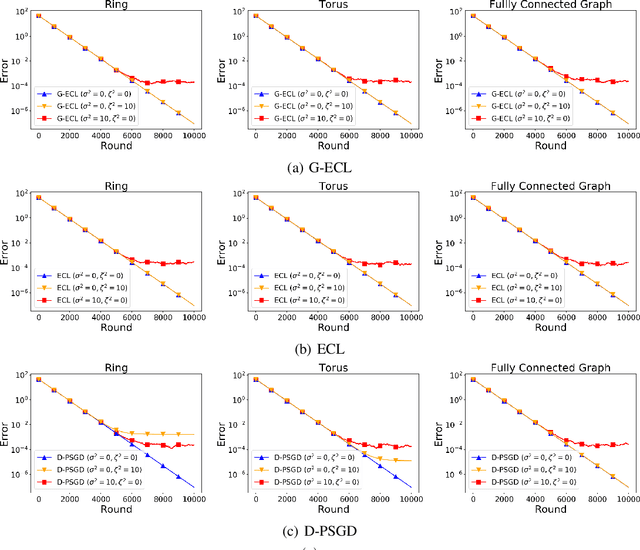
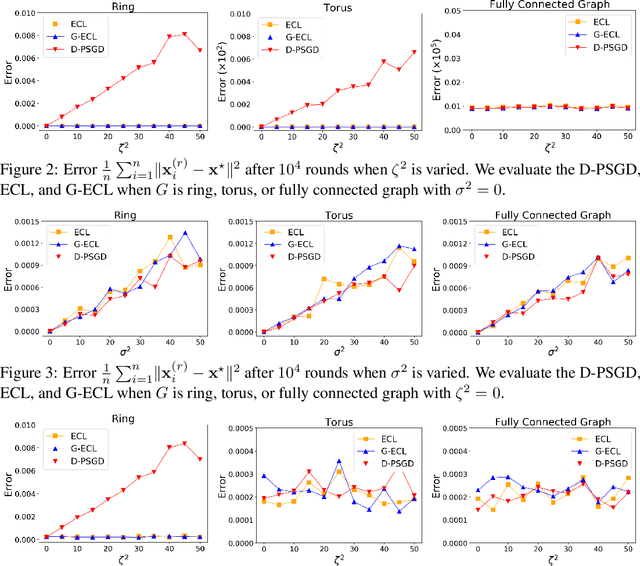
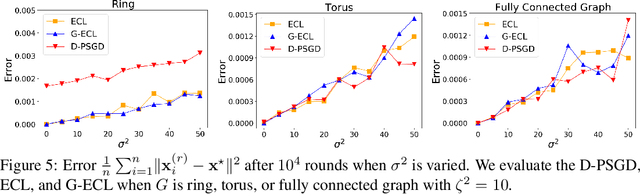
In recent years, decentralized learning has emerged as a powerful tool not only for large-scale machine learning, but also for preserving privacy. One of the key challenges in decentralized learning is that the data distribution held by each node is statistically heterogeneous. To address this challenge, the primal-dual algorithm called the Edge-Consensus Learning (ECL) was proposed and was experimentally shown to be robust to the heterogeneity of data distributions. However, the convergence rate of the ECL is provided only when the objective function is convex, and has not been shown in a standard machine learning setting where the objective function is non-convex. Furthermore, the intuitive reason why the ECL is robust to the heterogeneity of data distributions has not been investigated. In this work, we first investigate the relationship between the ECL and Gossip algorithm and show that the update formulas of the ECL can be regarded as correcting the local stochastic gradient in the Gossip algorithm. Then, we propose the Generalized ECL (G-ECL), which contains the ECL as a special case, and provide the convergence rates of the G-ECL in both (strongly) convex and non-convex settings, which do not depend on the heterogeneity of data distributions. Through synthetic experiments, we demonstrate that the numerical results of both the G-ECL and ECL coincide with the convergence rate of the G-ECL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge