The variation of the sum of edge lengths in linear arrangements of trees

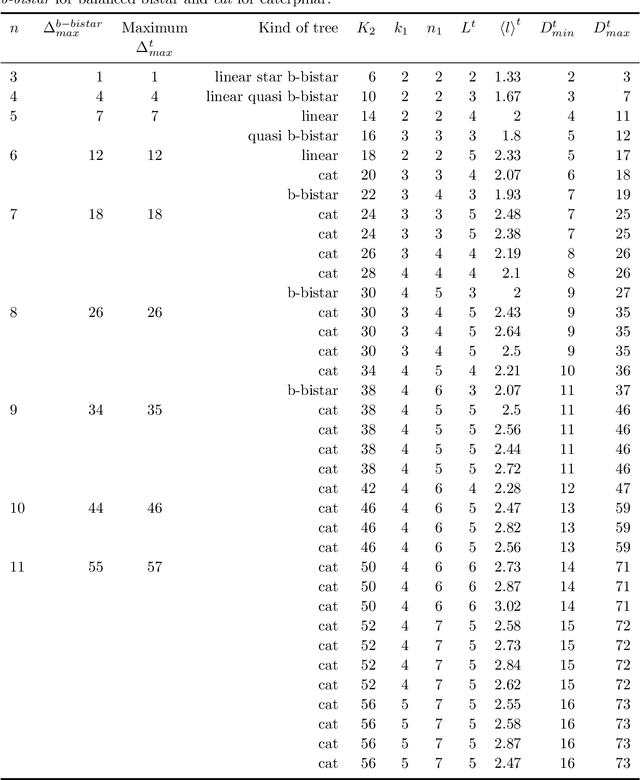
A fundamental problem in network science is the normalization of the topological or physical distance between vertices, that requires understanding the range of variation of the unnormalized distances. Here we investigate the limits of the variation of the physical distance in linear arrangements of the vertices of trees. In particular, we investigate various problems on the sum of edge lengths in trees of a fixed size: the minimum and the maximum value of the sum for specific trees, the minimum and the maximum in classes of trees (bistar trees and caterpillar trees) and finally the minimum and the maximum for any tree. We establish some foundations for research on optimality scores for spatial networks in one dimension.