The similarity metric
Paper and Code
Aug 05, 2004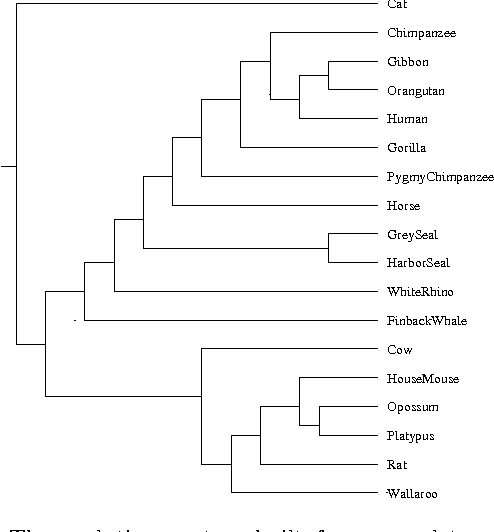
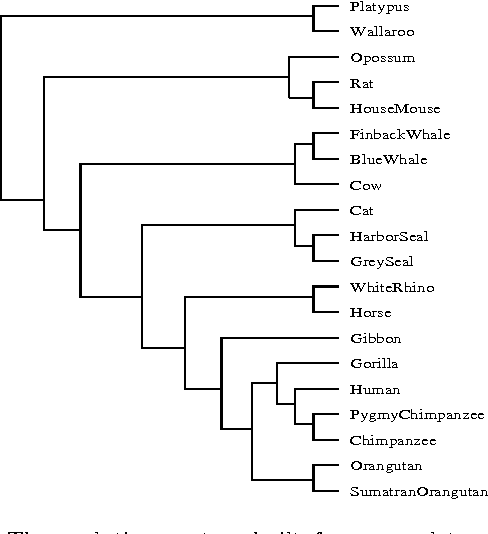
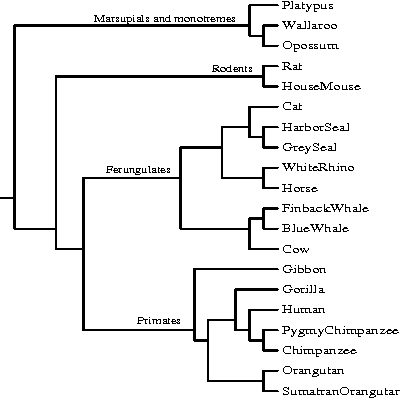
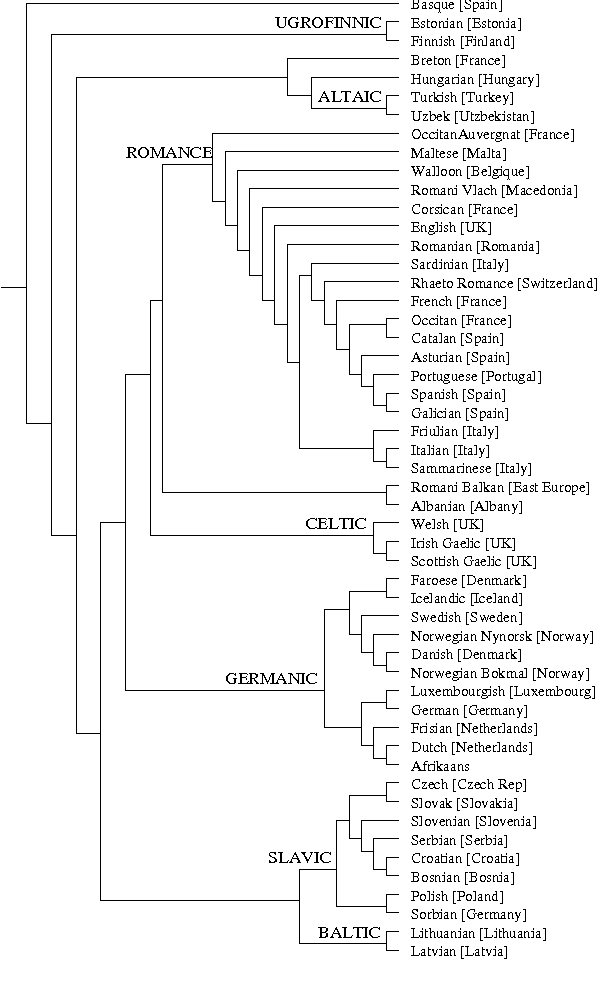
A new class of distances appropriate for measuring similarity relations between sequences, say one type of similarity per distance, is studied. We propose a new ``normalized information distance'', based on the noncomputable notion of Kolmogorov complexity, and show that it is in this class and it minorizes every computable distance in the class (that is, it is universal in that it discovers all computable similarities). We demonstrate that it is a metric and call it the {\em similarity metric}. This theory forms the foundation for a new practical tool. To evidence generality and robustness we give two distinctive applications in widely divergent areas using standard compression programs like gzip and GenCompress. First, we compare whole mitochondrial genomes and infer their evolutionary history. This results in a first completely automatic computed whole mitochondrial phylogeny tree. Secondly, we fully automatically compute the language tree of 52 different languages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge