The Privacy Blanket of the Shuffle Model

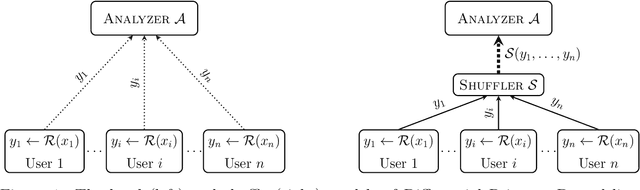
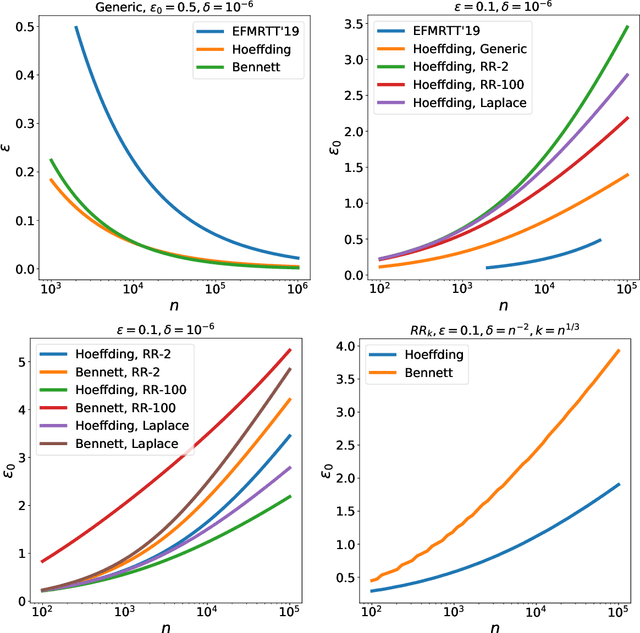
This work studies differential privacy in the context of the recently proposed shuffle model. Unlike in the local model, where the server collecting privatized data from users can track back an input to a specific user, in the shuffle model users submit their privatized inputs to a server anonymously. This setup yields a trust model which sits in between the classical curator and local models for differential privacy. The shuffle model is the core idea in the Encode, Shuffle, Analyze (ESA) model introduced by Bittau et al. (SOPS 2017). Recent work by Cheu et al. (Forthcoming, EUROCRYPT 2019) analyzes the differential privacy properties of the shuffle model and shows that in some cases shuffled protocols provide strictly better accuracy than local protocols. Additionally, Erlignsson et al. (SODA 2019) provide a privacy amplification bound quantifying the level of curator differential privacy achieved by the shuffle model in terms of the local differential privacy of the randomizer used by each user. In this context, we make three contributions. First, we provide an optimal single message protocol for summation of real numbers in the shuffle model. Our protocol is very simple and has better accuracy and communication than the protocols for this same problem proposed by Cheu et al. Optimality of this protocol follows from our second contribution, a new lower bound for the accuracy of private protocols for summation of real numbers in the shuffle model. The third contribution is a new amplification bound for analyzing the privacy of protocols in the shuffle model in terms of the privacy provided by the corresponding local randomizer. Our amplification bound generalizes the results by Erlingsson et al. to a wider range of parameters, and provides a whole family of methods to analyze privacy amplification in the shuffle model.