The Power of Regularization in Solving Extensive-Form Games
Paper and Code
Jun 19, 2022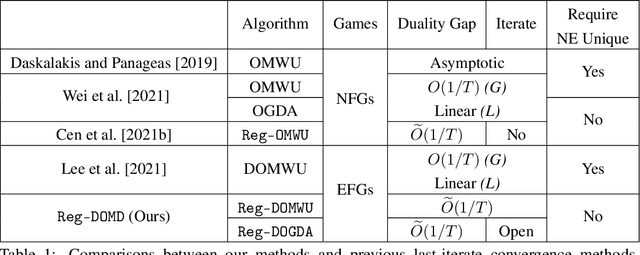
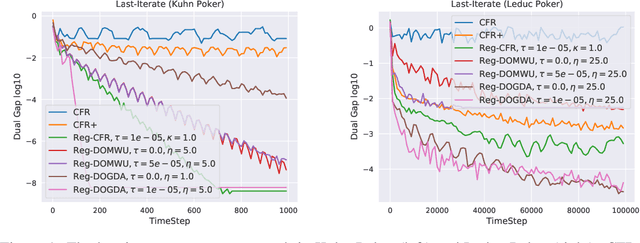
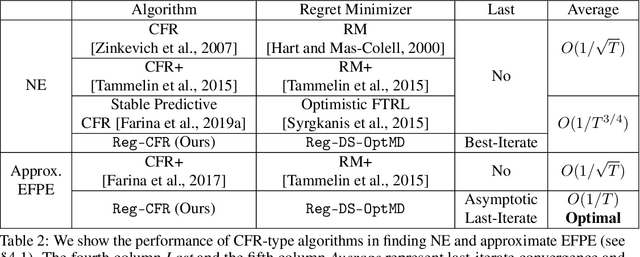
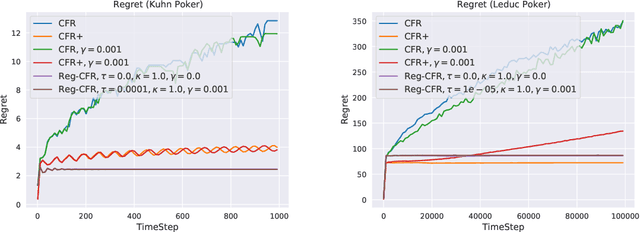
In this paper, we investigate the power of regularization, a common technique in reinforcement learning and optimization, in solving extensive-form games (EFGs). We propose a series of new algorithms based on regularizing the payoff functions of the game, and establish a set of convergence results that strictly improve over the existing ones, with either weaker assumptions or stronger convergence guarantees. In particular, we first show that dilated optimistic mirror descent (DOMD), an efficient variant of OMD for solving EFGs, with adaptive regularization can achieve a fast $\tilde O(1/T)$ last-iterate convergence in terms of duality gap without the uniqueness assumption of the Nash equilibrium (NE). Moreover, regularized dilated optimistic multiplicative weights update (Reg-DOMWU), an instance of Reg-DOMD, further enjoys the $\tilde O(1/T)$ last-iterate convergence rate of the distance to the set of NE. This addresses an open question on whether iterate convergence can be obtained for OMWU algorithms without the uniqueness assumption in both the EFG and normal-form game literature. Second, we show that regularized counterfactual regret minimization (Reg-CFR), with a variant of optimistic mirror descent algorithm as regret-minimizer, can achieve $O(1/T^{1/4})$ best-iterate, and $O(1/T^{3/4})$ average-iterate convergence rate for finding NE in EFGs. Finally, we show that Reg-CFR can achieve asymptotic last-iterate convergence, and optimal $O(1/T)$ average-iterate convergence rate, for finding the NE of perturbed EFGs, which is useful for finding approximate extensive-form perfect equilibria (EFPE). To the best of our knowledge, they constitute the first last-iterate convergence results for CFR-type algorithms, while matching the SOTA average-iterate convergence rate in finding NE for non-perturbed EFGs. We also provide numerical results to corroborate the advantages of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge