The Latent Structure of Dictionaries
Paper and Code
Jan 22, 2016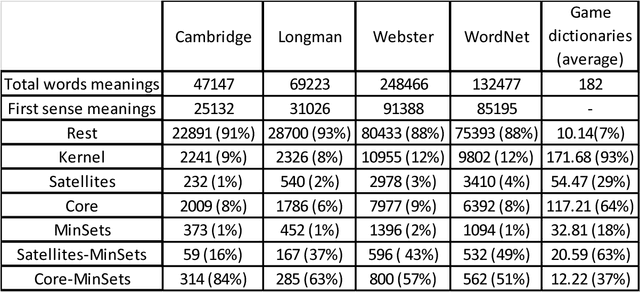
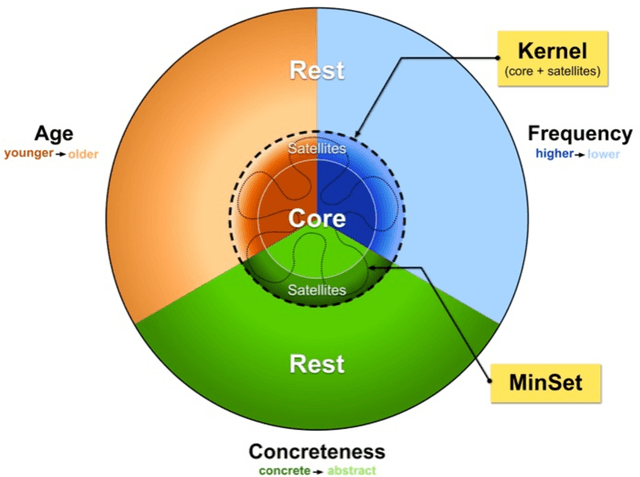
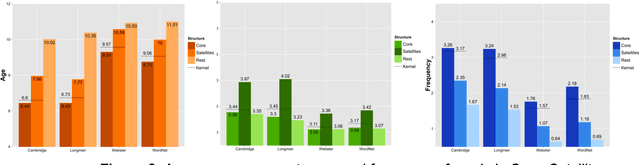
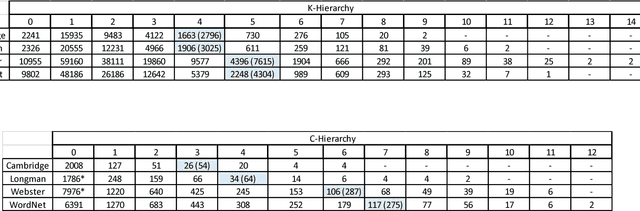
How many words (and which ones) are sufficient to define all other words? When dictionaries are analyzed as directed graphs with links from defining words to defined words, they reveal a latent structure. Recursively removing all words that are reachable by definition but that do not define any further words reduces the dictionary to a Kernel of about 10%. This is still not the smallest number of words that can define all the rest. About 75% of the Kernel turns out to be its Core, a Strongly Connected Subset of words with a definitional path to and from any pair of its words and no word's definition depending on a word outside the set. But the Core cannot define all the rest of the dictionary. The 25% of the Kernel surrounding the Core consists of small strongly connected subsets of words: the Satellites. The size of the smallest set of words that can define all the rest (the graph's Minimum Feedback Vertex Set or MinSet) is about 1% of the dictionary, 15% of the Kernel, and half-Core, half-Satellite. But every dictionary has a huge number of MinSets. The Core words are learned earlier, more frequent, and less concrete than the Satellites, which in turn are learned earlier and more frequent but more concrete than the rest of the Dictionary. In principle, only one MinSet's words would need to be grounded through the sensorimotor capacity to recognize and categorize their referents. In a dual-code sensorimotor-symbolic model of the mental lexicon, the symbolic code could do all the rest via re-combinatory definition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge