The Last-Iterate Convergence Rate of Optimistic Mirror Descent in Stochastic Variational Inequalities
Paper and Code
Jul 05, 2021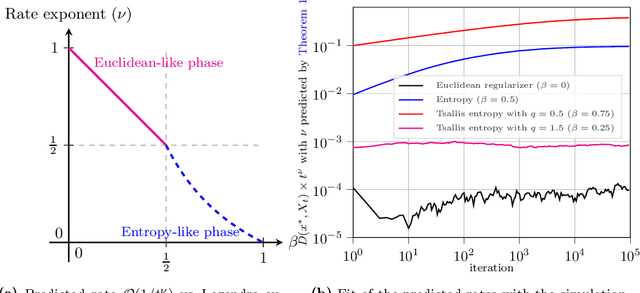
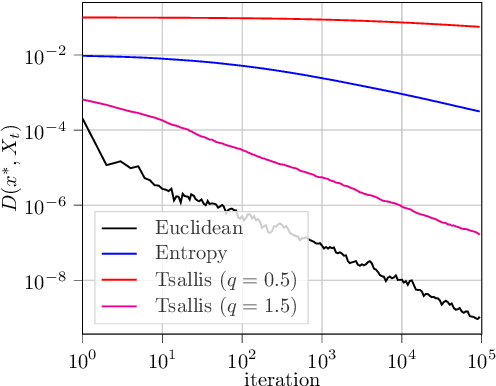
In this paper, we analyze the local convergence rate of optimistic mirror descent methods in stochastic variational inequalities, a class of optimization problems with important applications to learning theory and machine learning. Our analysis reveals an intricate relation between the algorithm's rate of convergence and the local geometry induced by the method's underlying Bregman function. We quantify this relation by means of the Legendre exponent, a notion that we introduce to measure the growth rate of the Bregman divergence relative to the ambient norm near a solution. We show that this exponent determines both the optimal step-size policy of the algorithm and the optimal rates attained, explaining in this way the differences observed for some popular Bregman functions (Euclidean projection, negative entropy, fractional power, etc.).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge