The Implicit Bias of Gradient Descent on Separable Data
Paper and Code
Mar 21, 2018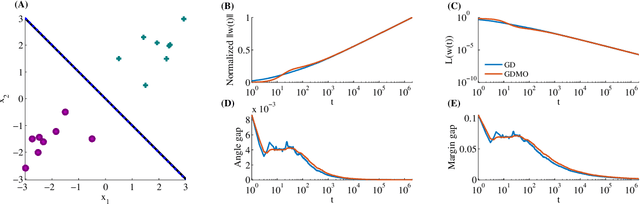
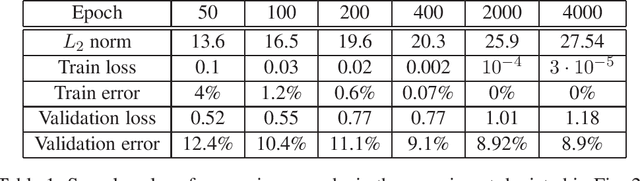
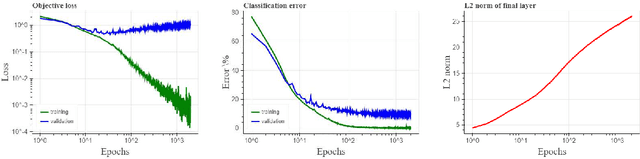
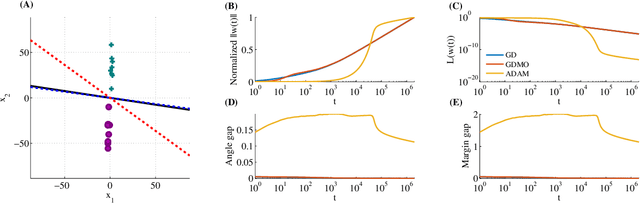
We show that gradient descent on an unregularized logistic regression problem, for linearly separable datasets, converges to the direction of the max-margin (hard margin SVM) solution. The result generalizes also to other monotone decreasing loss functions with an infimum at infinity, to multi-class problems, and to training a weight layer in a deep network in a certain restricted setting. Furthermore, we show this convergence is very slow, and only logarithmic in the convergence of the loss itself. This can help explain the benefit of continuing to optimize the logistic or cross-entropy loss even after the training error is zero and the training loss is extremely small, and, as we show, even if the validation loss increases. Our methodology can also aid in understanding implicit regularization in more complex models and with other optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge