The Fallacy of Minimizing Local Regret in the Sequential Task Setting
Paper and Code
Mar 16, 2024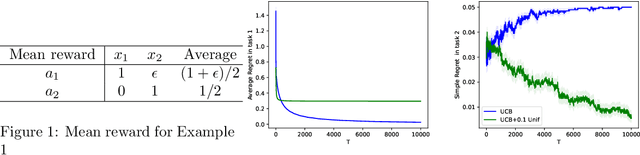
In the realm of Reinforcement Learning (RL), online RL is often conceptualized as an optimization problem, where an algorithm interacts with an unknown environment to minimize cumulative regret. In a stationary setting, strong theoretical guarantees, like a sublinear ($\sqrt{T}$) regret bound, can be obtained, which typically implies the convergence to an optimal policy and the cessation of exploration. However, these theoretical setups often oversimplify the complexities encountered in real-world RL implementations, where tasks arrive sequentially with substantial changes between tasks and the algorithm may not be allowed to adaptively learn within certain tasks. We study the changes beyond the outcome distributions, encompassing changes in the reward designs (mappings from outcomes to rewards) and the permissible policy spaces. Our results reveal the fallacy of myopically minimizing regret within each task: obtaining optimal regret rates in the early tasks may lead to worse rates in the subsequent ones, even when the outcome distributions stay the same. To realize the optimal cumulative regret bound across all the tasks, the algorithm has to overly explore in the earlier tasks. This theoretical insight is practically significant, suggesting that due to unanticipated changes (e.g., rapid technological development or human-in-the-loop involvement) between tasks, the algorithm needs to explore more than it would in the usual stationary setting within each task. Such implication resonates with the common practice of using clipped policies in mobile health clinical trials and maintaining a fixed rate of $\epsilon$-greedy exploration in robotic learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge