The Difficulty of Training Sparse Neural Networks
Paper and Code
Jul 17, 2019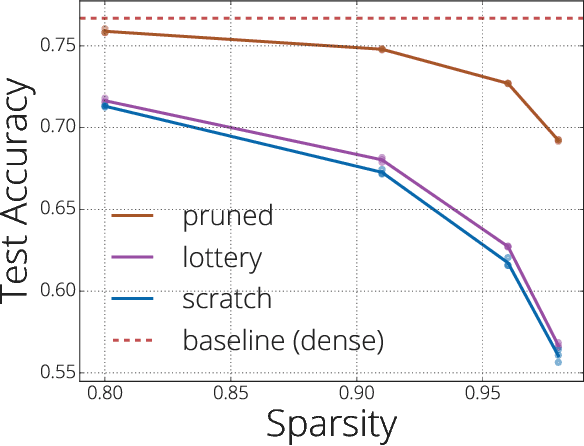
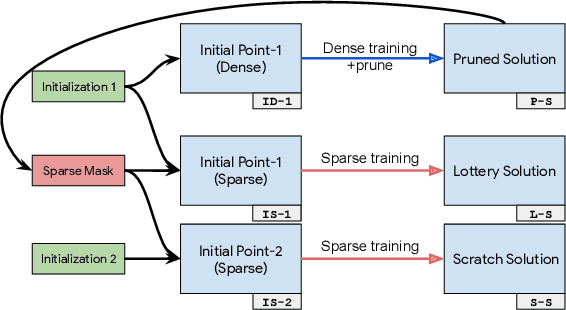
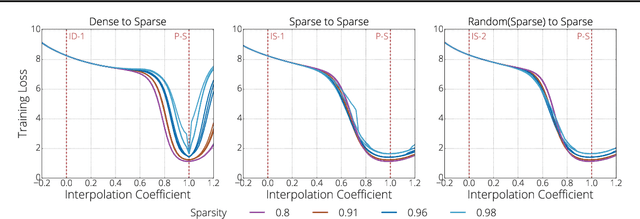
We investigate the difficulties of training sparse neural networks and make new observations about optimization dynamics and the energy landscape within the sparse regime. Recent work of \citep{Gale2019, Liu2018} has shown that sparse ResNet-50 architectures trained on ImageNet-2012 dataset converge to solutions that are significantly worse than those found by pruning. We show that, despite the failure of optimizers, there is a linear path with a monotonically decreasing objective from the initialization to the "good" solution. Additionally, our attempts to find a decreasing objective path from "bad" solutions to the "good" ones in the sparse subspace fail. However, if we allow the path to traverse the dense subspace, then we consistently find a path between two solutions. These findings suggest traversing extra dimensions may be needed to escape stationary points found in the sparse subspace.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge