The Complexity of Reasoning with Global Constraints
Paper and Code
Mar 06, 2009
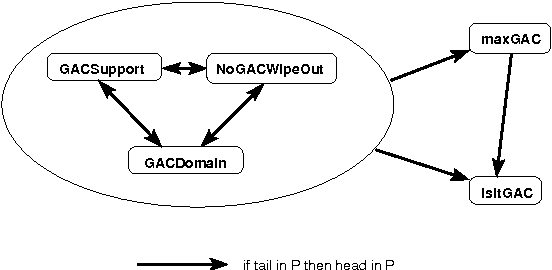
Constraint propagation is one of the techniques central to the success of constraint programming. To reduce search, fast algorithms associated with each constraint prune the domains of variables. With global (or non-binary) constraints, the cost of such propagation may be much greater than the quadratic cost for binary constraints. We therefore study the computational complexity of reasoning with global constraints. We first characterise a number of important questions related to constraint propagation. We show that such questions are intractable in general, and identify dependencies between the tractability and intractability of the different questions. We then demonstrate how the tools of computational complexity can be used in the design and analysis of specific global constraints. In particular, we illustrate how computational complexity can be used to determine when a lesser level of local consistency should be enforced, when constraints can be safely generalized, when decomposing constraints will reduce the amount of pruning, and when combining constraints is tractable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge