The Bregman Variational Dual-Tree Framework
Paper and Code
Sep 26, 2013


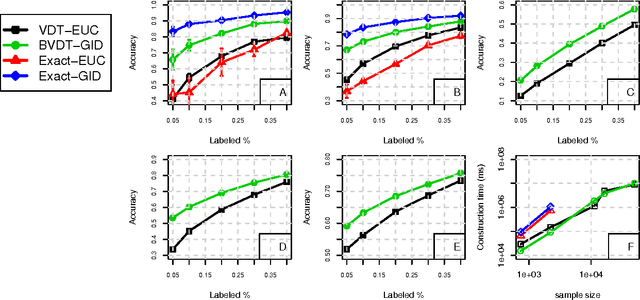
Graph-based methods provide a powerful tool set for many non-parametric frameworks in Machine Learning. In general, the memory and computational complexity of these methods is quadratic in the number of examples in the data which makes them quickly infeasible for moderate to large scale datasets. A significant effort to find more efficient solutions to the problem has been made in the literature. One of the state-of-the-art methods that has been recently introduced is the Variational Dual-Tree (VDT) framework. Despite some of its unique features, VDT is currently restricted only to Euclidean spaces where the Euclidean distance quantifies the similarity. In this paper, we extend the VDT framework beyond the Euclidean distance to more general Bregman divergences that include the Euclidean distance as a special case. By exploiting the properties of the general Bregman divergence, we show how the new framework can maintain all the pivotal features of the VDT framework and yet significantly improve its performance in non-Euclidean domains. We apply the proposed framework to different text categorization problems and demonstrate its benefits over the original VDT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge