The Benefit of Multitask Representation Learning
Paper and Code
Mar 25, 2016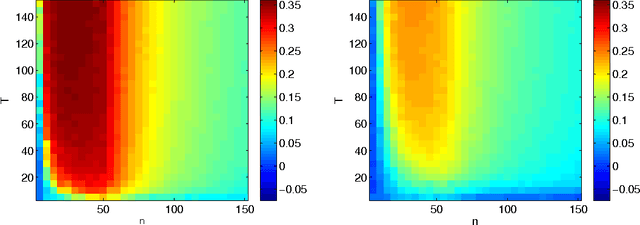
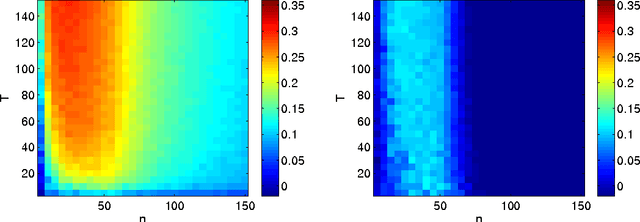
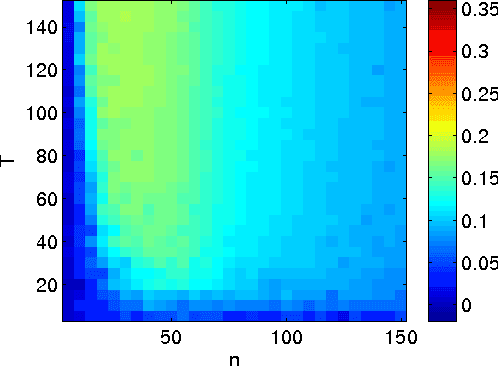
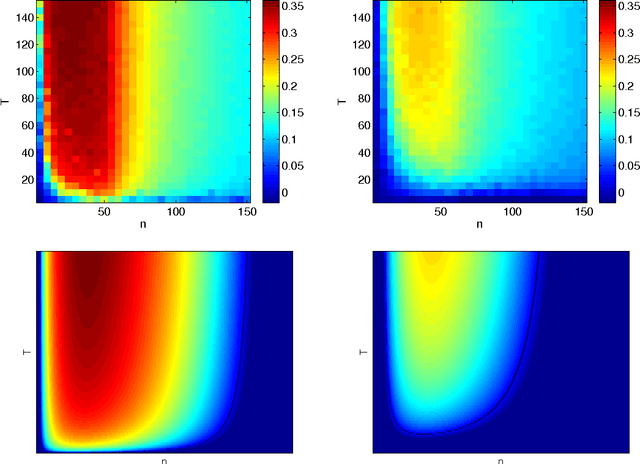
We discuss a general method to learn data representations from multiple tasks. We provide a justification for this method in both settings of multitask learning and learning-to-learn. The method is illustrated in detail in the special case of linear feature learning. Conditions on the theoretical advantage offered by multitask representation learning over independent task learning are established. In particular, focusing on the important example of half-space learning, we derive the regime in which multitask representation learning is beneficial over independent task learning, as a function of the sample size, the number of tasks and the intrinsic data dimensionality. Other potential applications of our results include multitask feature learning in reproducing kernel Hilbert spaces and multilayer, deep networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge