Testing Identity of Multidimensional Histograms
Paper and Code
Apr 10, 2018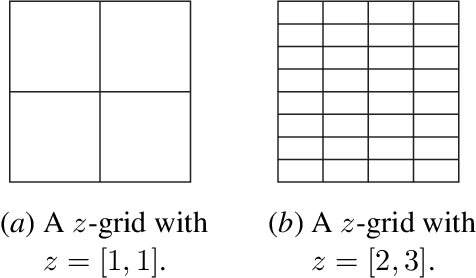
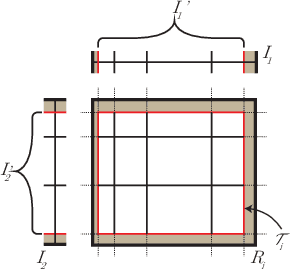
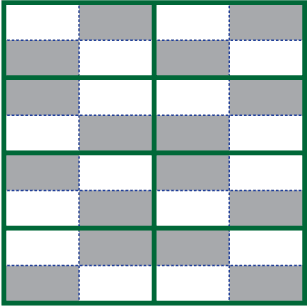

We investigate the problem of identity testing for multidimensional histogram distributions. A distribution $p: D \rightarrow \mathbb{R}_+$, where $D \subseteq \mathbb{R}^d$, is called a {$k$-histogram} if there exists a partition of the domain into $k$ axis-aligned rectangles such that $p$ is constant within each such rectangle. Histograms are one of the most fundamental non-parametric families of distributions and have been extensively studied in computer science and statistics. We give the first identity tester for this problem with {\em sub-learning} sample complexity in any fixed dimension and a nearly-matching sample complexity lower bound. More specifically, let $q$ be an unknown $d$-dimensional $k$-histogram and $p$ be an explicitly given $k$-histogram. We want to correctly distinguish, with probability at least $2/3$, between the case that $p = q$ versus $\|p-q\|_1 \geq \epsilon$. We design a computationally efficient algorithm for this hypothesis testing problem with sample complexity $O((\sqrt{k}/\epsilon^2) \log^{O(d)}(k/\epsilon))$. Our algorithm is robust to model misspecification, i.e., succeeds even if $q$ is only promised to be {\em close} to a $k$-histogram. Moreover, for $k = 2^{\Omega(d)}$, we show a nearly-matching sample complexity lower bound of $\Omega((\sqrt{k}/\epsilon^2) (\log(k/\epsilon)/d)^{\Omega(d)})$ when $d\geq 2$. Prior to our work, the sample complexity of the $d=1$ case was well-understood, but no algorithm with sub-learning sample complexity was known, even for $d=2$. Our new upper and lower bounds have interesting conceptual implications regarding the relation between learning and testing in this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge