Tensor Completion via Gaussian Process Based Initialization
Paper and Code
Dec 11, 2019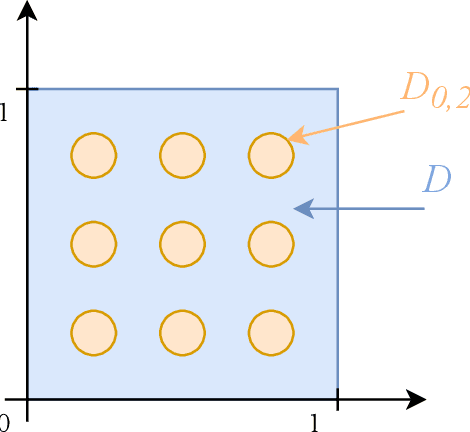
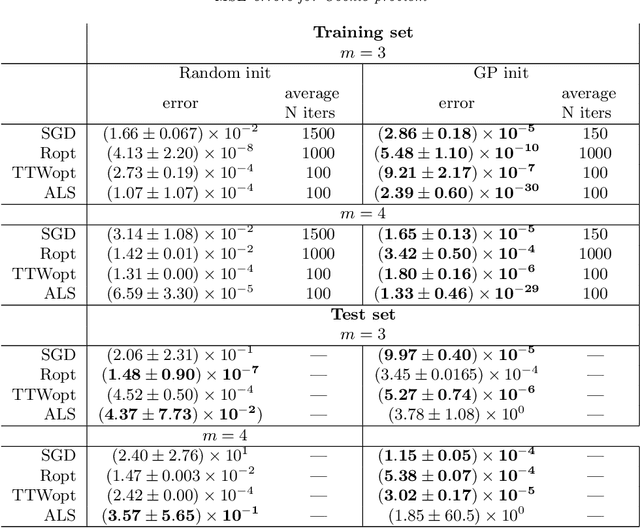
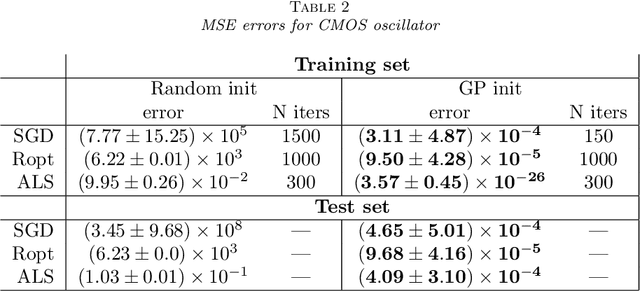
In this paper, we consider the tensor completion problem representing the solution in the tensor train (TT) format. It is assumed that tensor is high-dimensional, and tensor values are generated by an unknown smooth function. The assumption allows us to develop an efficient initialization scheme based on Gaussian Process Regression and TT-cross approximation technique. The proposed approach can be used in conjunction with any optimization algorithm that is usually utilized in tensor completion problems. We empirically justify that in this case the reconstruction error improves compared to the tensor completion with random initialization. As an additional benefit, our technique automatically selects rank thanks to using the TT-cross approximation technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge