Temporal Energy Analysis of Symbol Sequences for Fiber Nonlinear Interference Modelling via Energy Dispersion Index
Paper and Code
Feb 24, 2021
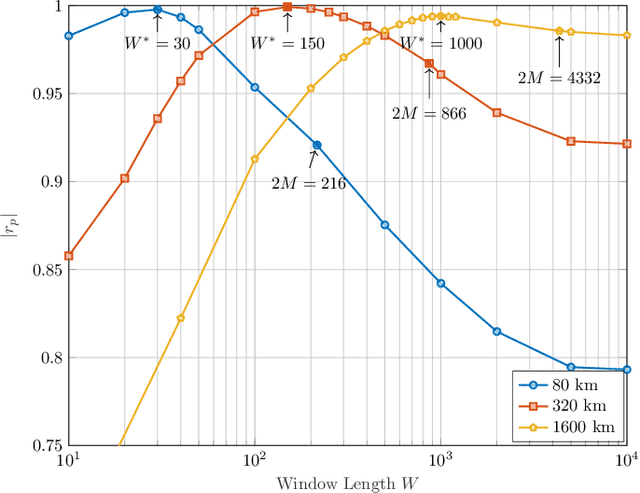

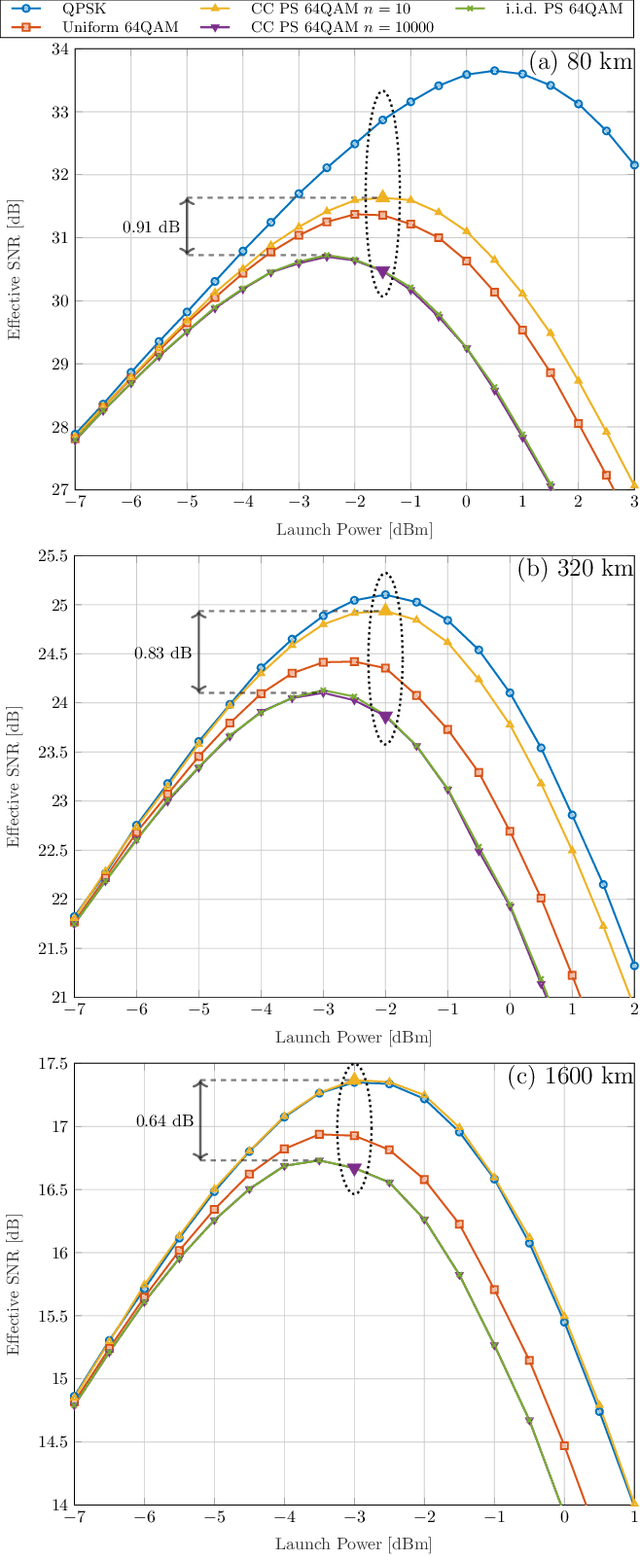
The stationary statistical properties of independent, identically distributed (i.i.d.) input symbols provide insights on the induced nonlinear interference (NLI) during fiber transmission. For example, kurtosis is known to predict the modulation format-dependent NLI. These statistical properties can be used in the design of probabilistic amplitude shaping (PAS), which is a popular scheme that relies on an amplitude shaper for increasing spectral efficiencies of fiber-optic systems. One property of certain shapers used in PAS -- including constant-composition distribution matchers -- that is often overlooked is that a time-dependency between amplitudes is introduced. This dependency results in symbols that are non-i.i.d., which have time-varying statistical properties. Somewhat surprisingly, the effective signal-to-noise ratio (SNR) in PAS has been shown to increase when the shaping blocklength decreases. This blocklength dependency of SNR has been attributed to time-varying statistical properties of the symbol sequences, in particular, to variation of the symbol energies. In this paper, we investigate the temporal energy behavior of symbol sequences, and introduce a new metric called energy dispersion index (EDI). EDI captures the time-varying statistical properties of symbol energies. Numerical results show strong correlations between EDI and effective SNR, with absolute correlation coefficients above 99% for different transmission distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge