TD or not TD: Analyzing the Role of Temporal Differencing in Deep Reinforcement Learning
Paper and Code
Jun 04, 2018

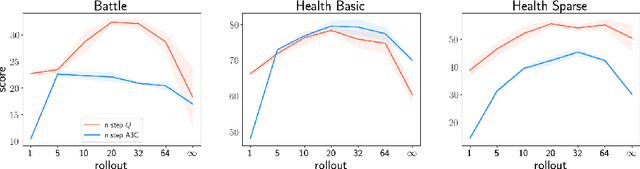
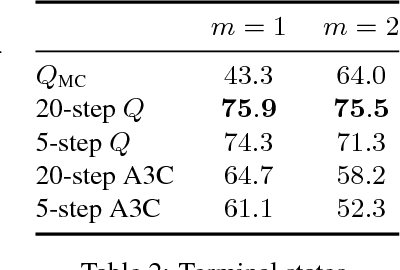
Our understanding of reinforcement learning (RL) has been shaped by theoretical and empirical results that were obtained decades ago using tabular representations and linear function approximators. These results suggest that RL methods that use temporal differencing (TD) are superior to direct Monte Carlo estimation (MC). How do these results hold up in deep RL, which deals with perceptually complex environments and deep nonlinear models? In this paper, we re-examine the role of TD in modern deep RL, using specially designed environments that control for specific factors that affect performance, such as reward sparsity, reward delay, and the perceptual complexity of the task. When comparing TD with infinite-horizon MC, we are able to reproduce classic results in modern settings. Yet we also find that finite-horizon MC is not inferior to TD, even when rewards are sparse or delayed. This makes MC a viable alternative to TD in deep RL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge