Systematic Generalization in Neural Networks-based Multivariate Time Series Forecasting Models
Paper and Code
Mar 07, 2021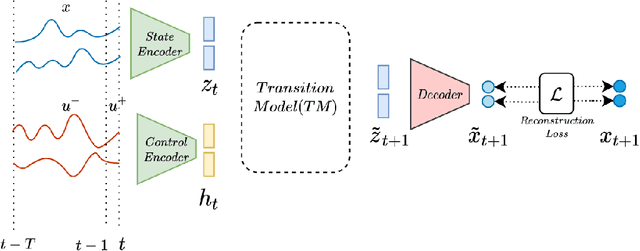
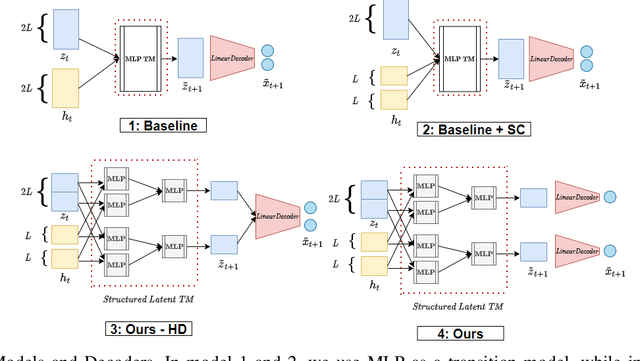
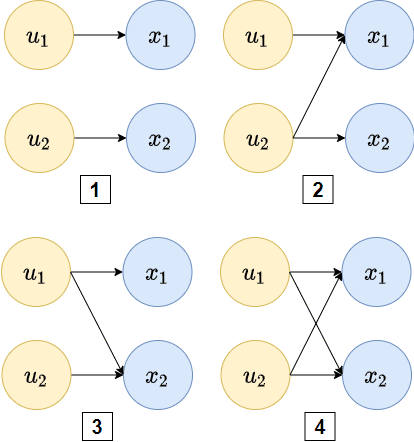
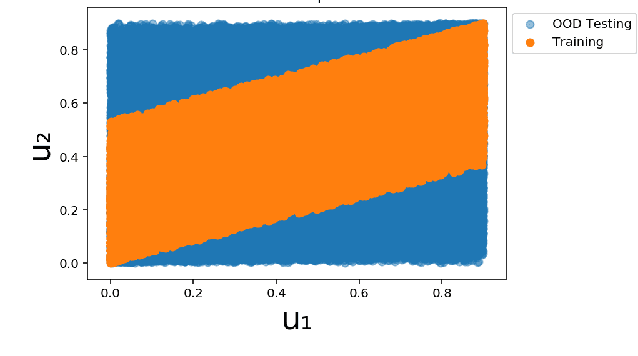
Systematic generalization aims to evaluate reasoning about novel combinations from known components, an intrinsic property of human cognition. In this work, we study systematic generalization of NNs in forecasting future time series of dependent variables in a dynamical system, conditioned on past time series of dependent variables, and past and future control variables. We focus on systematic generalization wherein the NN-based forecasting model should perform well on previously unseen combinations or regimes of control variables after being trained on a limited set of the possible regimes. For NNs to depict such out-of-distribution generalization, they should be able to disentangle the various dependencies between control variables and dependent variables. We hypothesize that a modular NN architecture guided by the readily-available knowledge of independence of control variables as a potentially useful inductive bias to this end. Through extensive empirical evaluation on a toy dataset and a simulated electric motor dataset, we show that our proposed modular NN architecture serves as a simple yet highly effective inductive bias that enabling better forecasting of the dependent variables up to large horizons in contrast to standard NNs, and indeed capture the true dependency relations between the dependent and the control variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge